合併排序法(Merge Sorting)

合併排序法是針對已排序好的二個或二個以上的數列，經由合併方式，組合成一個大的且已排好的數列。就像是前面一開始提到的分治法概念。

他的步驟大概如:

1.將含有n個元素的序列分割成含有n/2個長度的子序列

2.排序分割後的n/4個長度的子序列

3.合併排序完成的兩子序列，成為一個長度為n的序列

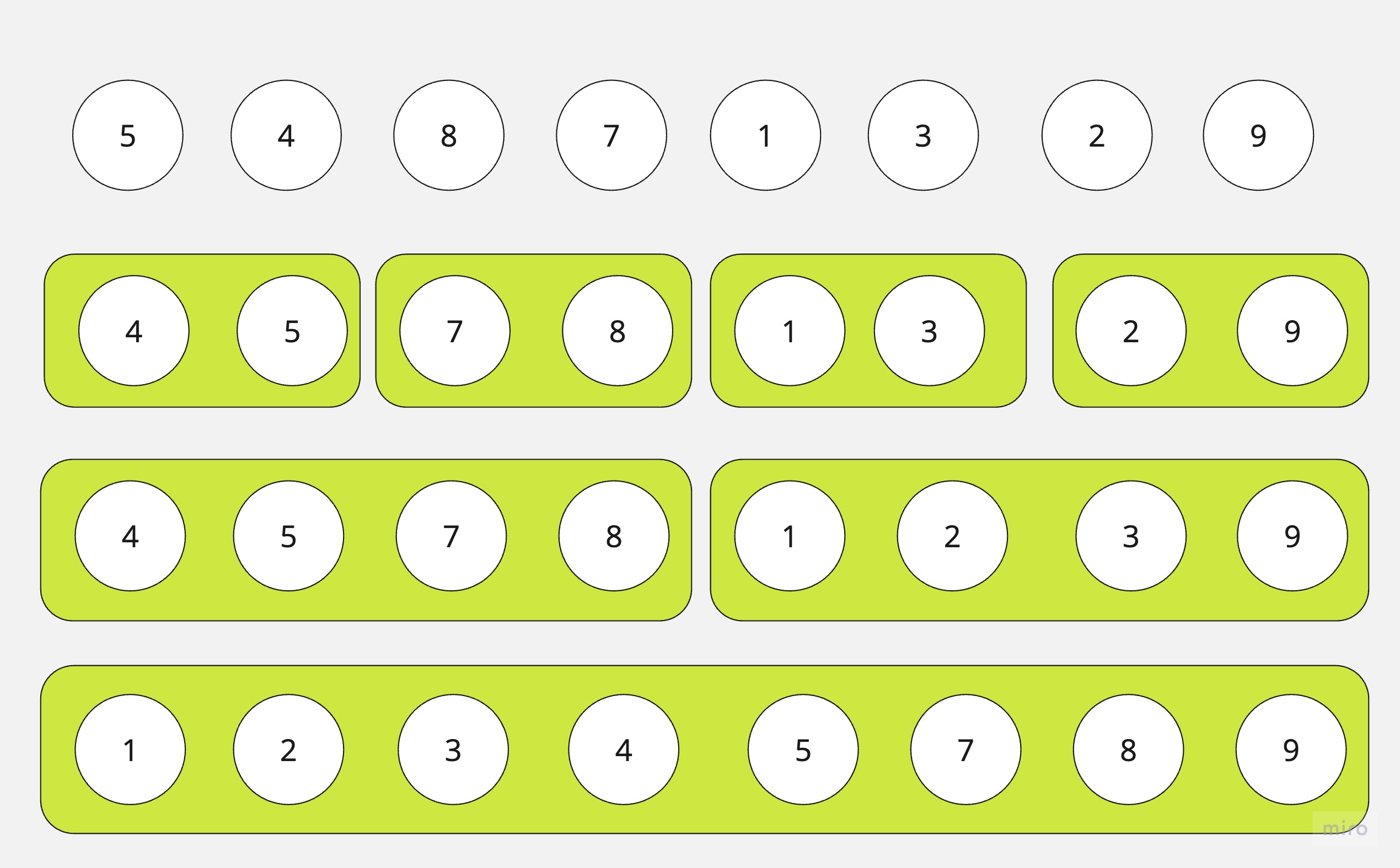
範例: 用選擇排序法將下面數列做排序:

    5,4,8,7,1,3,2,9

fn main() {
    let mut arr = vec![5, 4, 8, 7, 1, 3, 2, 9];
    merge_sort(&mut arr);
    println!("最後排序的數列:{:?}", arr);
}

fn merge_sort(arr: &mut Vec<i32>) {
    // 設定終止條件，arr為0長度不大於1
    if arr.len() <= 1 {
        return;
    }

    let mid = arr.len() / 2;
    let mut left = arr[..mid].to_vec();
    let mut right = arr[mid..].to_vec();

    merge_sort(&mut left);
    merge_sort(&mut right);

    let mut i = 0;
    let mut j = 0;
    let mut k = 0;

    while i < left.len() && j < right.len() {
        if left[i] <= right[j] {
            arr[k] = left[i];
            i += 1;
        } else {
            arr[k] = right[j];
            j += 1;
        }
        k += 1;
    }

    while i < left.len() {
        arr[k] = left[i];
        i += 1;
        k += 1;
    }

    while j < right.len() {
        arr[k] = right[j];
        j += 1;
        k += 1;
    }
    println!("每次置換的數列:{:?}", arr);
}

快速排序法(Quicksort)

快速排序是公認最佳的排序法，同樣也是分治法概念，在資料中找到一個隨機設定的虛擬中間值，並依此中間值將所有打算排序的資料分為兩部份。小於中間值的資料自左邊，大於中間值的資料放在右邊，再以同樣方式處理左右的資料，直到排序完成。

主要分三個步驟:

1.選擇:在序列中任選一個元素，稱為Pivit。

2.分割序列: 將序列重新排序，分為兩部份，比Pivot小的元素置換到pivot之前，比它大的元素換到它後面，而他自己會落在他最終的位置。

3.遞迴:分別將比pivot小及比pivot大兩部分重複上述步驟，直到新序列的長度小於等於1，無法繼續分割為止，就完成排序。

下面用此數列來排序:

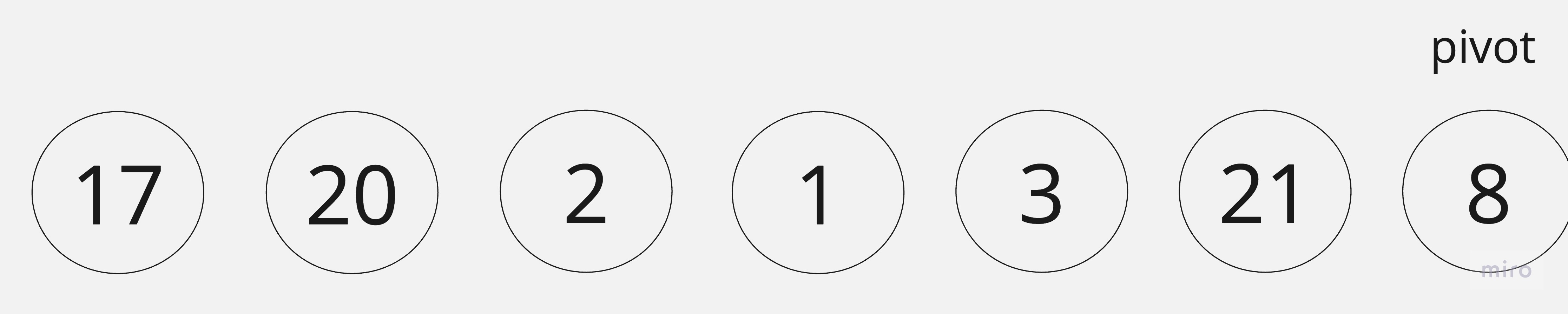
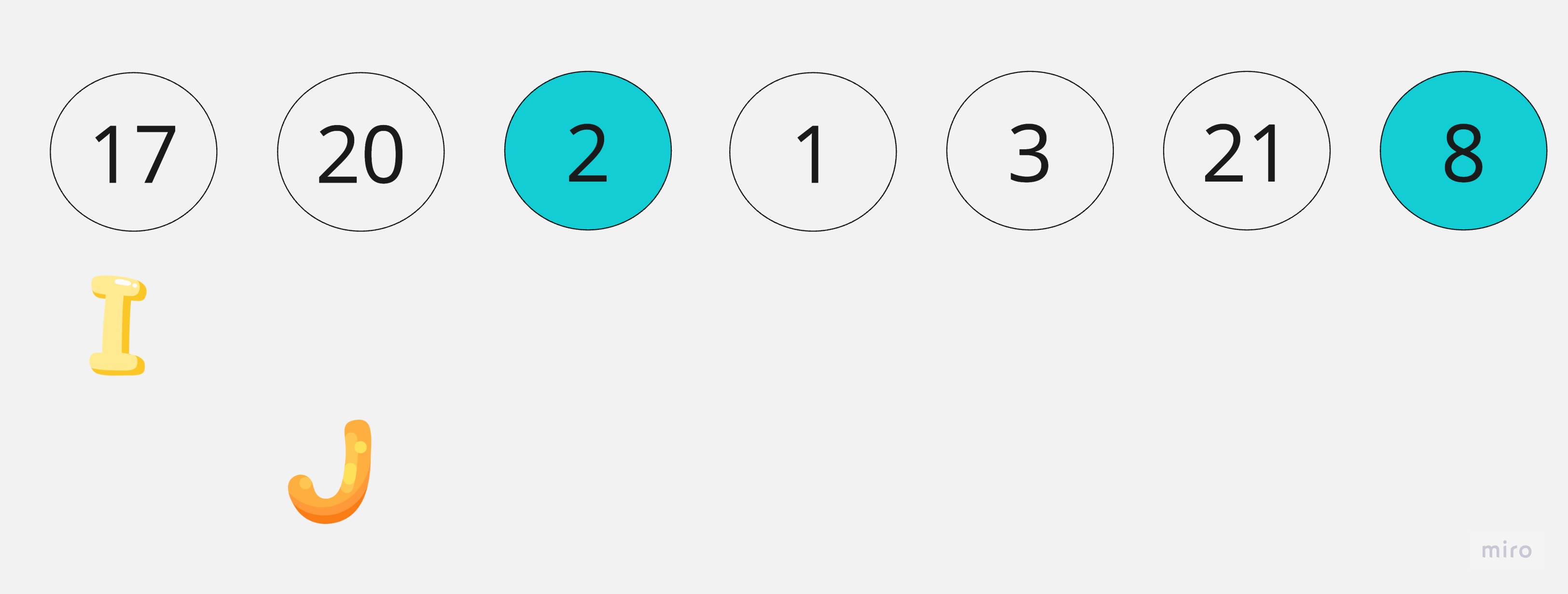
給訂一個序列，選擇最後一個元素作pivot，i,j在第一個元素位置。

第j個元素17大於8，所以不動。

第j個元素20大於8，所以不動。

第j個元素2小於8，一次更換i,j。i會往後一個位置。

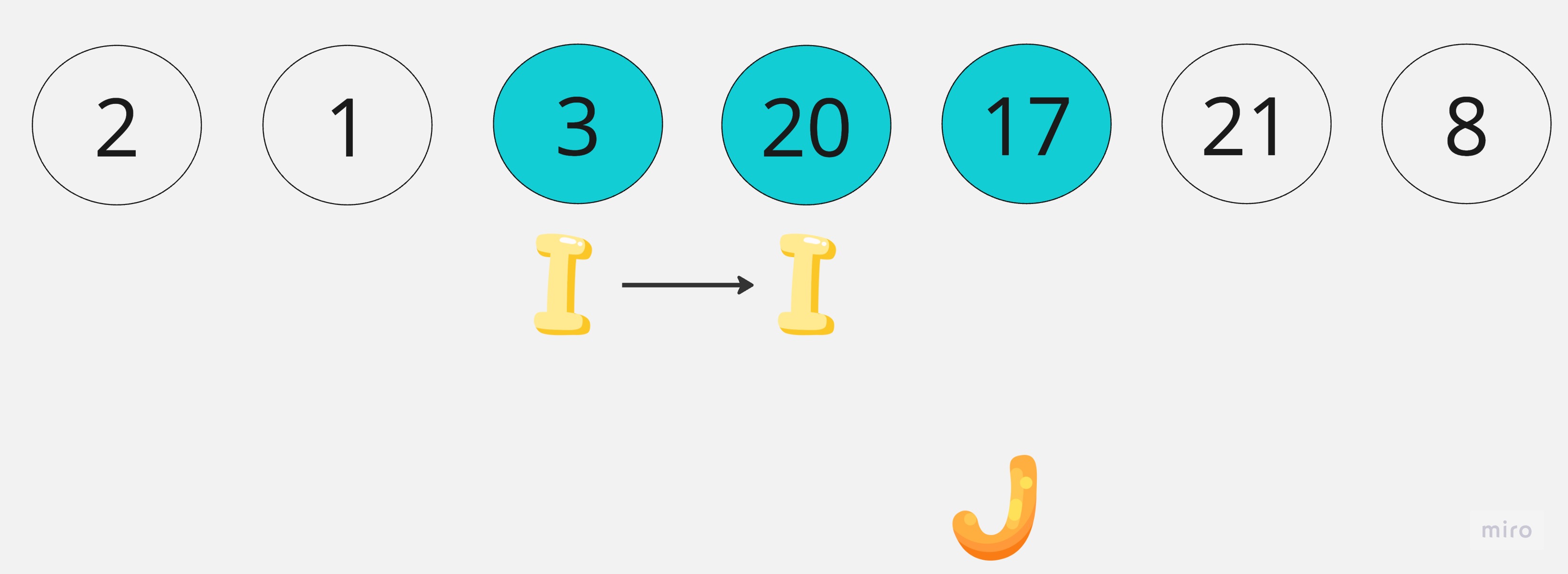
第j個元素21大於8，所以不動。

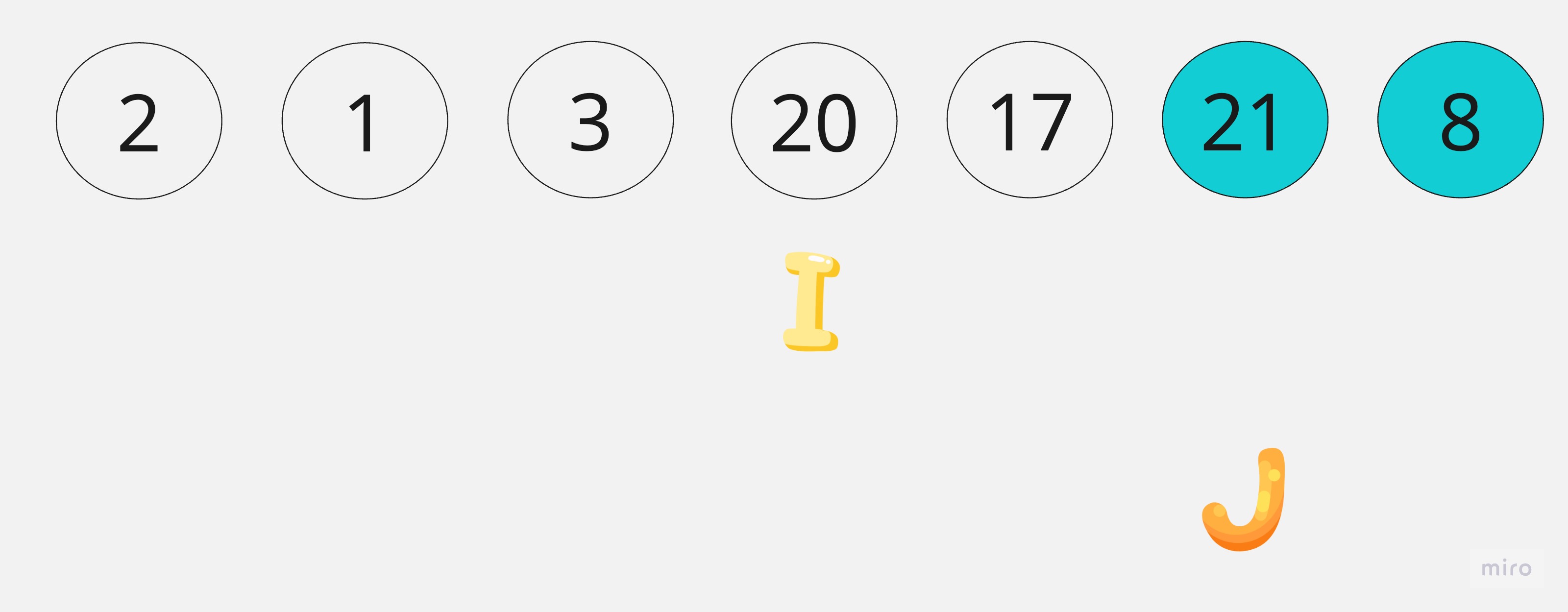
最後將pivot與i個元素交換，這時pivot已經在最後的位置上，前面的元素皆小於8，後面元素皆大於8。

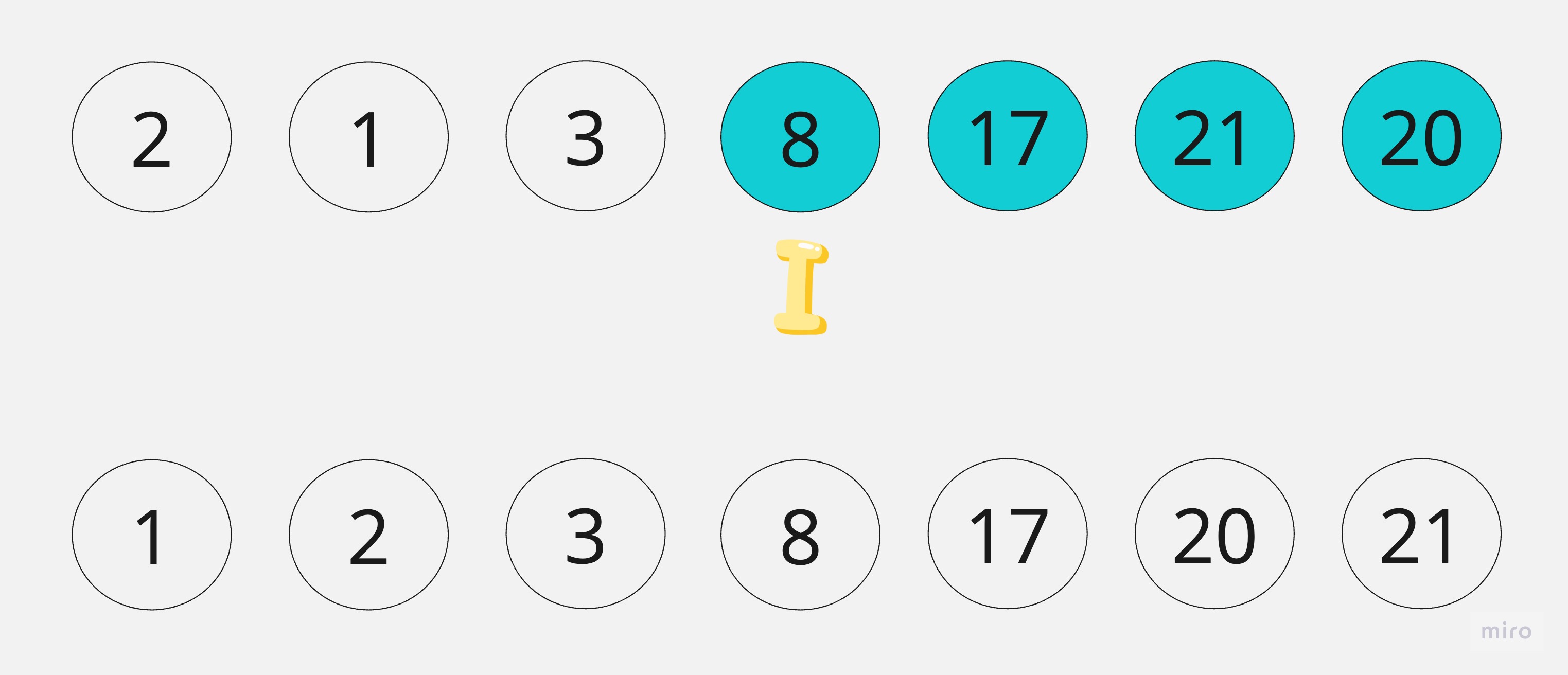
最後再遞迴分割就可完成陣列。

範例: 用快速排序法將下面數列做排序:

    [17,20,2,1,3,21,8]

fn main() {
    let mut arr = vec![17, 20, 2, 1, 3, 21, 8];
    let len = arr.len();
    quick_sort(&mut arr, 0, len - 1);
    println!("最後排序的數列: {:?}", arr);
}

fn quick_sort(arr: &mut Vec<i32>, low: usize, high: usize) {
    if low < high {
        let pivot_index = partition(arr, low, high);
        if pivot_index > 0 {
            quick_sort(arr, low, pivot_index - 1);
        }
        quick_sort(arr, pivot_index + 1, high);
    }
    
}

fn partition(arr: &mut Vec<i32>, low: usize, high: usize) -> usize {
    let pivot = arr[high];
    let mut i = low;
    for j in low..high {
        if arr[j] < pivot {
            arr.swap(i, j);
            i += 1;
        }
    }
    println!("每次置換的數列:{:?}", arr);
    arr.swap(i, high);
    i
}

堆積排序法(Heapsort)

堆積排序就像是選擇排序，但跟他不同的事利用堆積這種方式來排序。

堆積排序的特性:

• 使用堆積資料結構輔助，通常使用二元法堆積。

• 不穩定排序:排序後相同鍵值的元素相對位置可能改變。

• 原地排序:不需額外花費儲存空間來排序。

• 較差的CPU catch: 不連續存取位址的特性，不利於CPU快取。

以這個為排序的序列，將以遞增方向排序

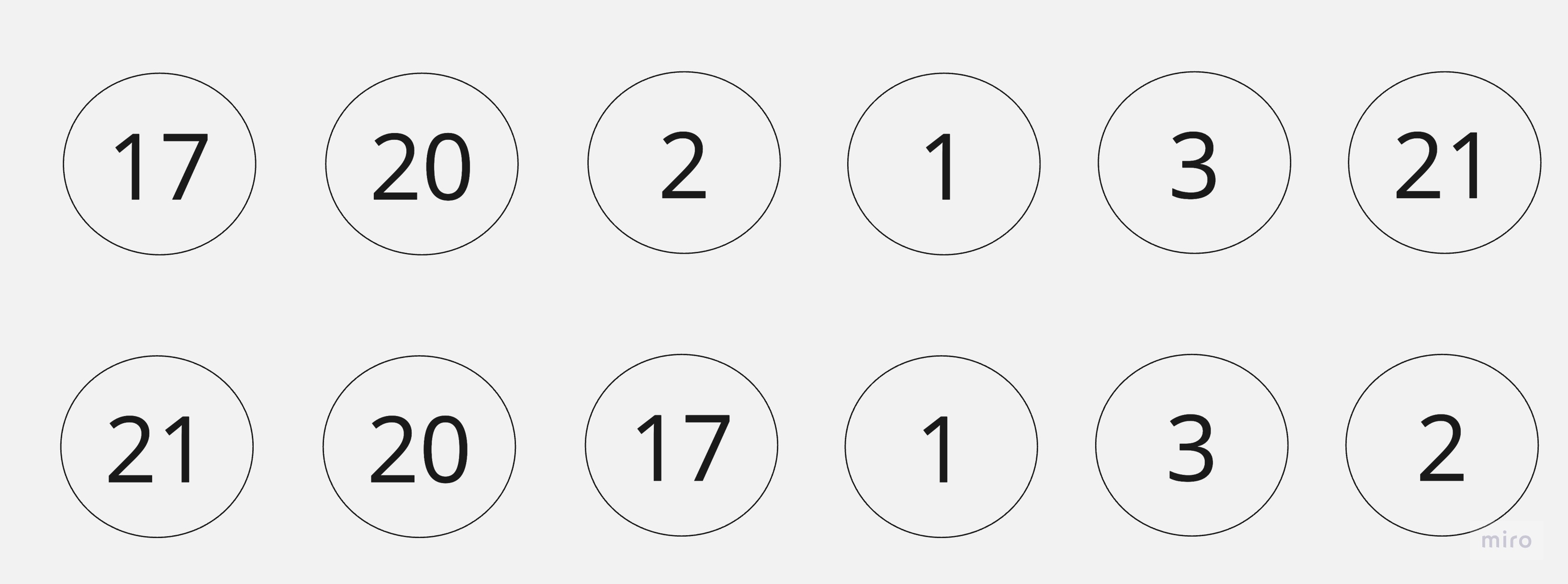
將資料轉為堆積資料結構

他對應的二元樹:

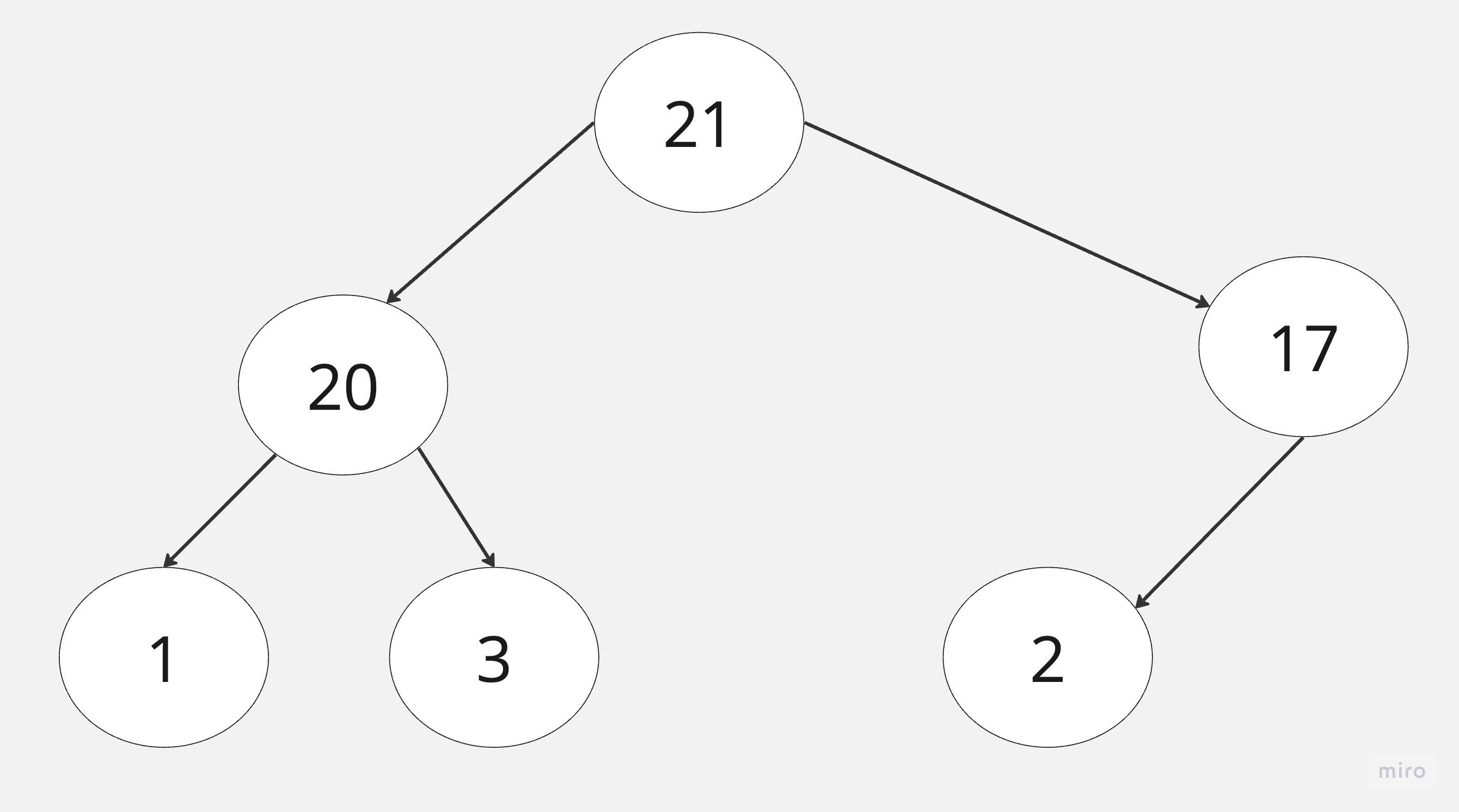
再來就是排序的部分，會將最大元素擺在root位置，我們先將最後一個節點與root進行交換，完成第一步。

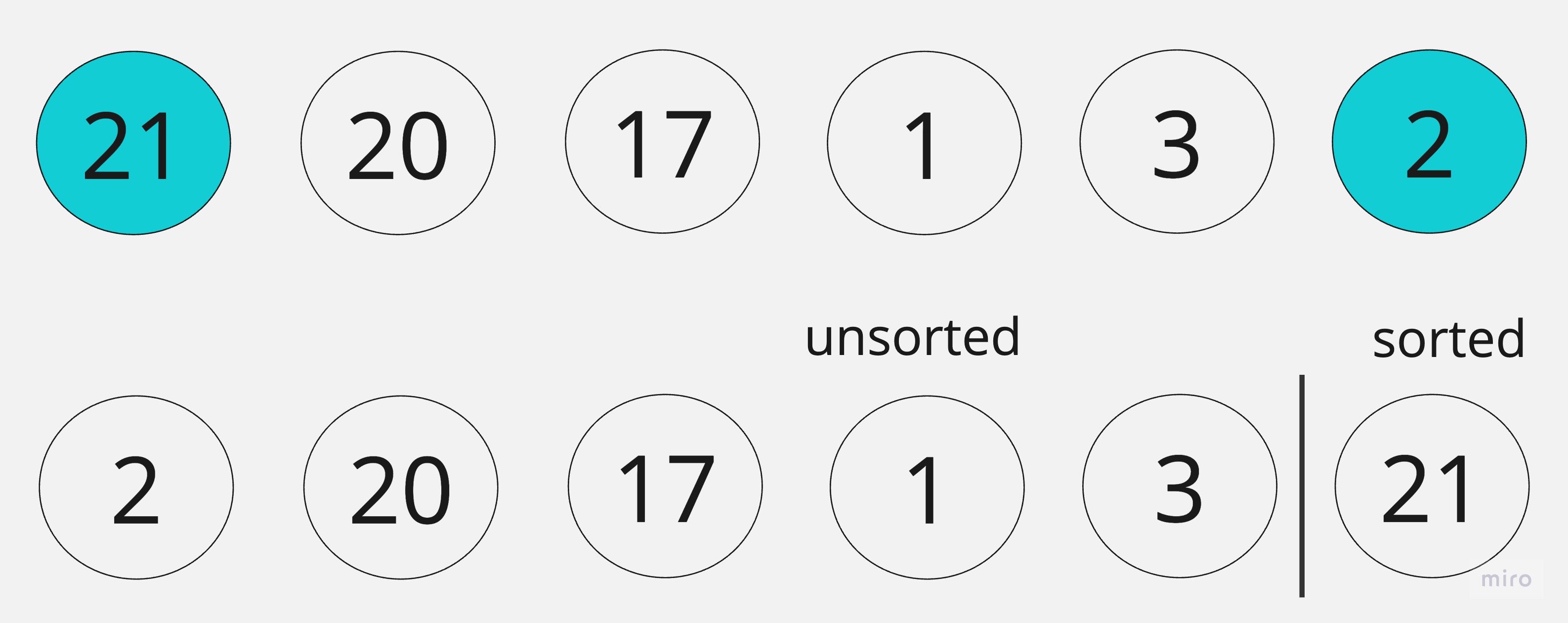
再來將為排序的資料區塊從整為符合最大堆積的結構。

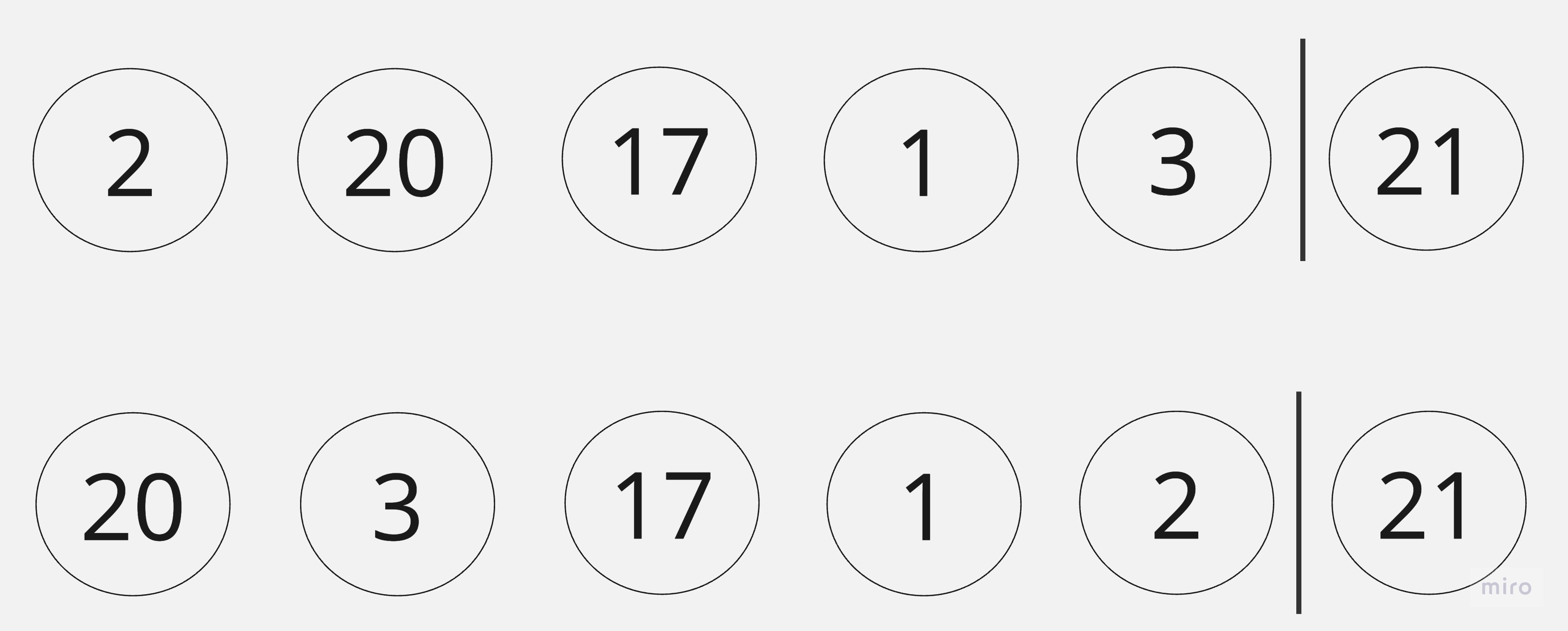
只要不斷的將root和最後一個節點交換，並將剩餘資料修正至滿足，就可完成排序。

這就是堆積排序的流程，就很像選擇排序法。

範例: 用插入排序法將下面數列做排序:

[17, 20, 2, 1, 3, 21]

fn main() {
    let mut arr = vec![17, 20, 2, 1, 3, 21];
    heap_sort(&mut arr);
    println!("最後排序的數列: {:?}", arr);
}

fn heap_sort(arr: &mut Vec<i32>) {
    let len = arr.len();
    
    // 最大堆
    for i in (0..len / 2).rev() {
        heapify(arr, len, i);
    }
    
    // 從堆積中取元素排序
    for i in (0..len).rev() {
        arr.swap(0, i);
        heapify(arr, i, 0);
    }
}

fn heapify(arr: &mut Vec<i32>, n: usize, i: usize) {
    let mut largest = i;
    let left = 2 * i + 1;
    let right = 2 * i + 2;
    
    if left < n && arr[left] > arr[largest] {
        largest = left;
    }
    
    if right < n && arr[right] > arr[largest] {
        largest = right;
    }
    
    if largest != i {
        arr.swap(i, largest);
        heapify(arr, n, largest);
    }
    println!("每次置換的數列:{:?}", arr);
}

插入排序法(Insert sort)

插入排序法是將陣列中的元素，逐一與排序好的資料做比較，前兩個元素先排好，再將第三個元素插入適當位置。當這三個元素排序好，接著再將第四個元素加入，重複此步驟，直到排序完成。

這邊就走一次演算流程:

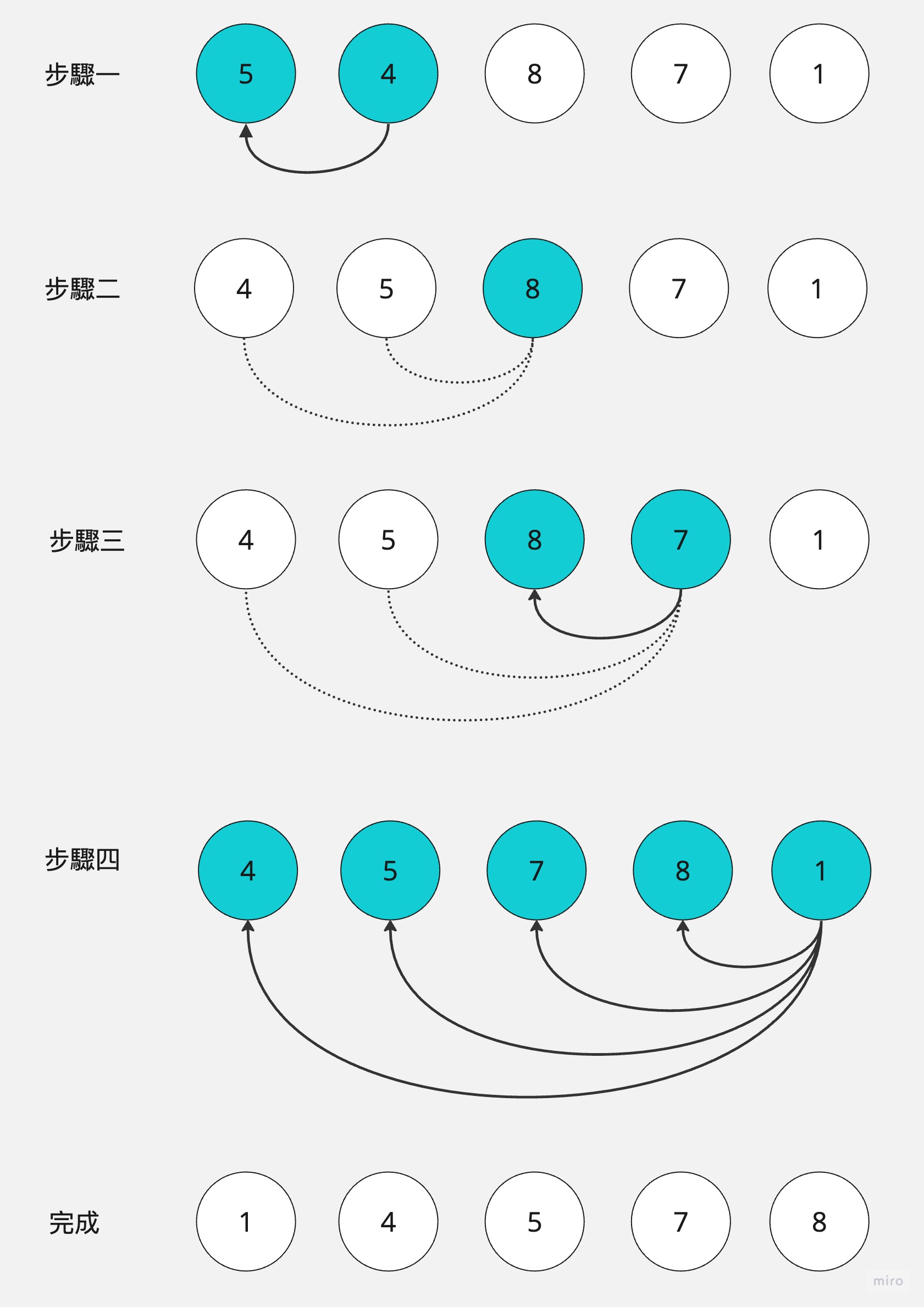
步驟一4先跟第一個元素比較，放到5前面，步驟二8跟前面兩個元素比較因為比較大所以不動，步驟三7跟前面三個元素比較，因為比8小所以移動但比前面兩個大所以就沒再往前移動，最後步驟四1跟前面的元素比較，所以移到最前面即完成排序。

範例: 用插入排序法將下面數列做排序:

    5,4,8,7,1

fn main() {
    let mut arr = [5, 4, 8, 7, 1];
    let n = arr.len();

    for i in 1..n {
        let mut j = i;

        while j > 0 && arr[i] < arr[j -1] {
            let temp = arr[i];
            arr[j] = arr [j - 1];
            arr[j - 1] = temp;
            j -= 1;
        }
            println!("每次置換的數列:{:?}", arr);
    }
    println!("排序後的數列: {:?}", arr);
}

希爾排序法(Shell Sort)

希爾排序法可以減少插入排序法中資料搬移的次數，插入排序法效率偏低，因為每次只能將數據移動一位。原理是將資料區分成特定間隔的幾個小區塊，以插入排序法排完區塊內的資料在減少間隔距離。

演算流程:

1.我們用gap sequence來排序，首先算出第一個gap為(8/2)=4

先排序(5,4)，這邊(3,9)所以不動，再來排序(8,6)，接著(7,2)

2.算出第二個gap為8/2 * 2=2

先排序4,6所以不動，接著3,2，接著(6,5)，再來是(3,9),(6,8)所以不動，接著(9,7)

3.算出第三次。gap為8/222=1，但前一次結果已經很接近排序完成，這邊就可以完成。

範例:

用希爾排序法將下面數列做排序:

[5, 3, 8, 7, 4, 9, 6, 2]

fn main() {
    let mut arr = [5, 3, 8, 7, 4, 9, 6, 2];
    let n = arr.len();
    
    let mut gap = n / 2;
    
    while gap > 0 {
        for i in gap..n {
            let mut j = i;
            let current = arr[i];
            
            while j >= gap && arr[j - gap] > current {
                arr[j] = arr[j - gap];
                j -= gap;
            }
            
            arr[j] = current;
        }
        
        gap /= 2;
        println!("每次置換的數列:{:?}", arr);
    }

    println!("最後排序的數列:{:?}", arr);
}