河內塔演算法(Tower of Hanoil)

法國數學家Lucas發明了河內塔這個數學問題，典型使用遞迴式與堆疊來解決此問題。古越南某間是廟有三根銀棒(有些故事是木樁)，要把某些數量大小不同的圓盤從第一個銀棒移動到第三個。

問題是:假設有A,B,C三個銀棒和n個大小均不相同的圓盤，由小到大編號1,2,3…n，編號越大直徑越大。開始時，n個圓盤是在A銀棒上，要將A銀棒上的圓盤藉著B銀棒當中間橋樑，全部移到C銀棒上最少次的方法，不過在移動時有規則:

1. 直徑較小的圓盤永遠放在直徑較大的圓盤上

2. 圓盤可任意地由任何一個銀棒移到其他銀棒上

3. 每一次僅能移動一個圓盤，而且只能從最上面的圓盤開始移動

我這邊用n=1~3的狀況來走一次河內塔的步驟:

• n=1 個圓盤

直接把圓盤從1號銀棒移動到3號銀棒

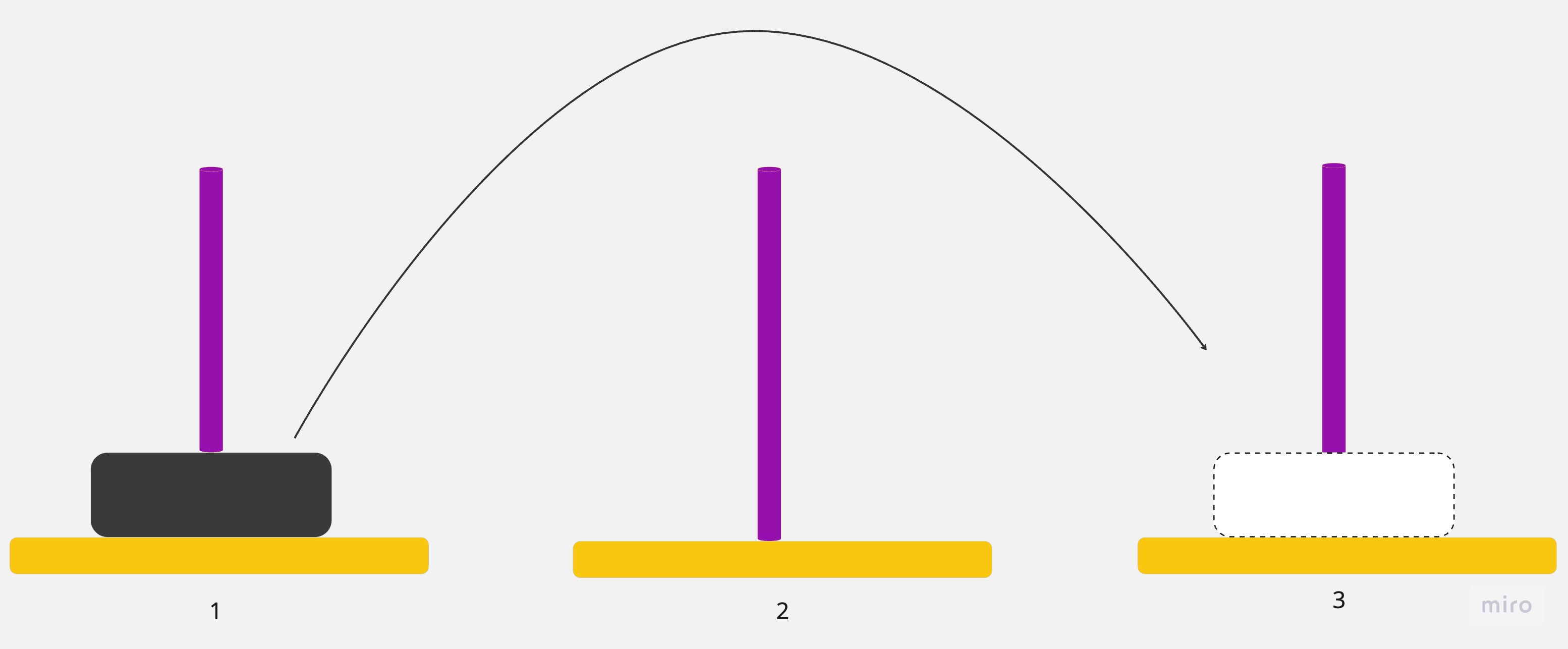
• n=2 個圓盤

1.將圓盤從1號銀棒移到2號銀棒

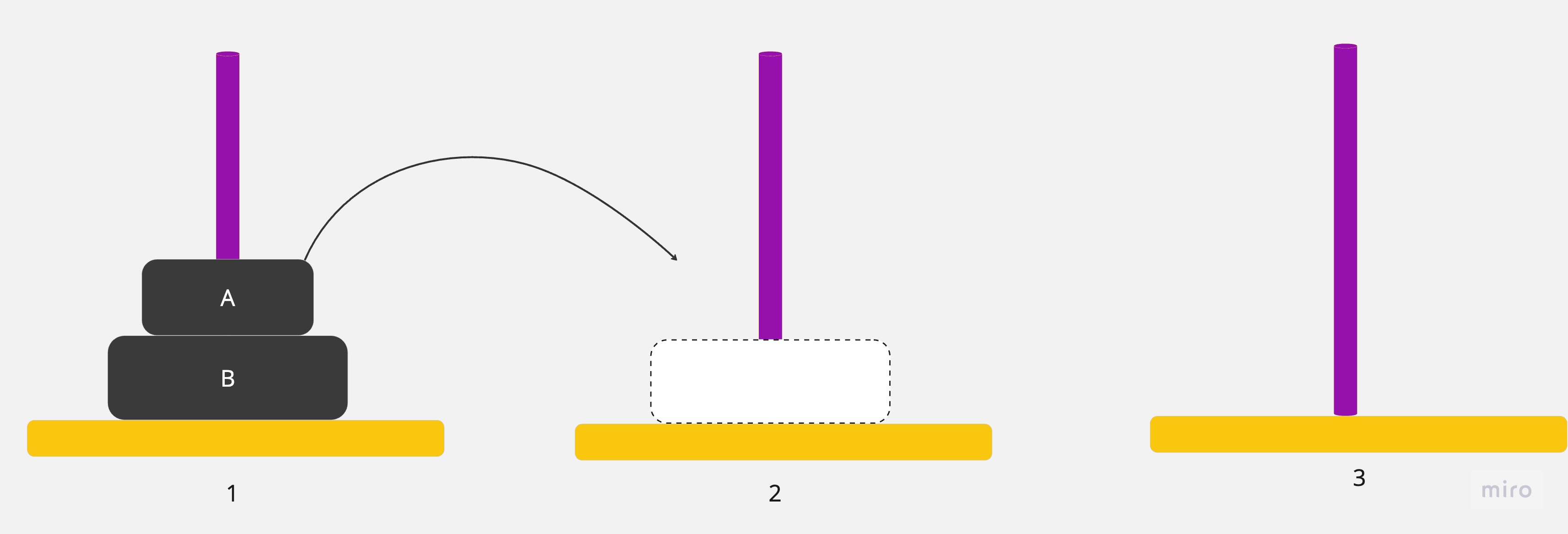
2.將圓盤從1號銀棒移到3號銀棒

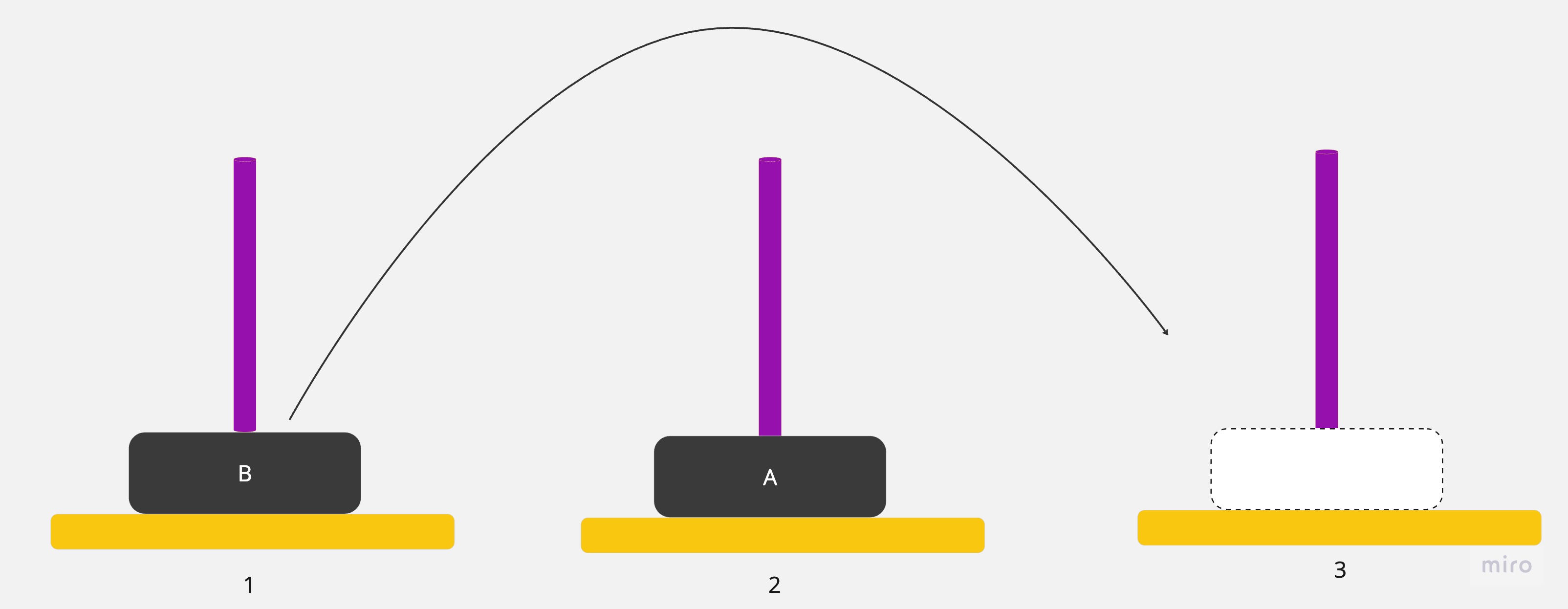
3.將圓盤從2號銀棒移到3號銀棒，就完成了。

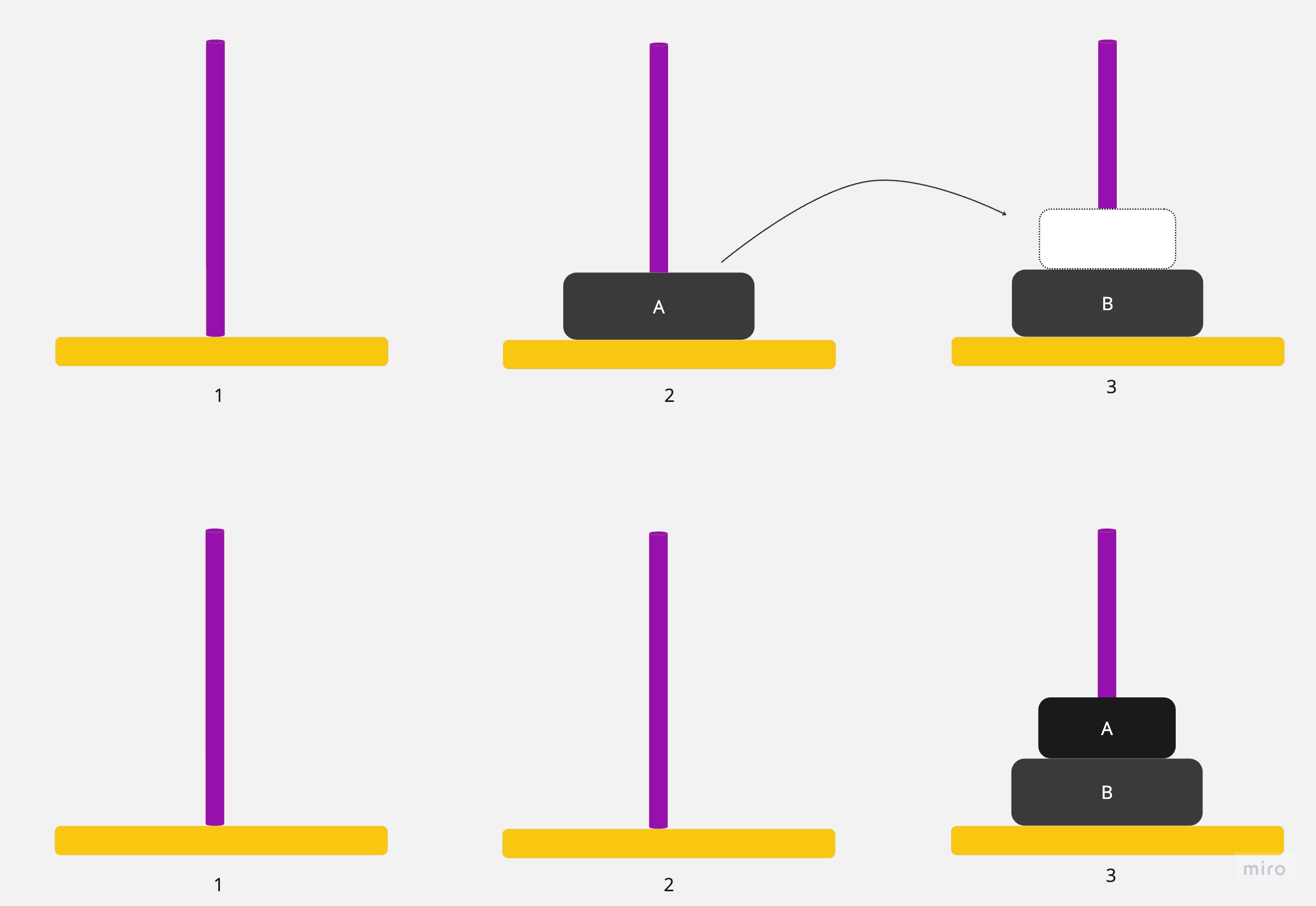
結論:移動了2^2-1=3次，圓盤移的順序為1,2,1(圓盤次序)

步驟:1>2,1>3,2>3(銀棒次序)

• n=3個圓盤

1.將圓盤從1號銀棒移到3號銀棒

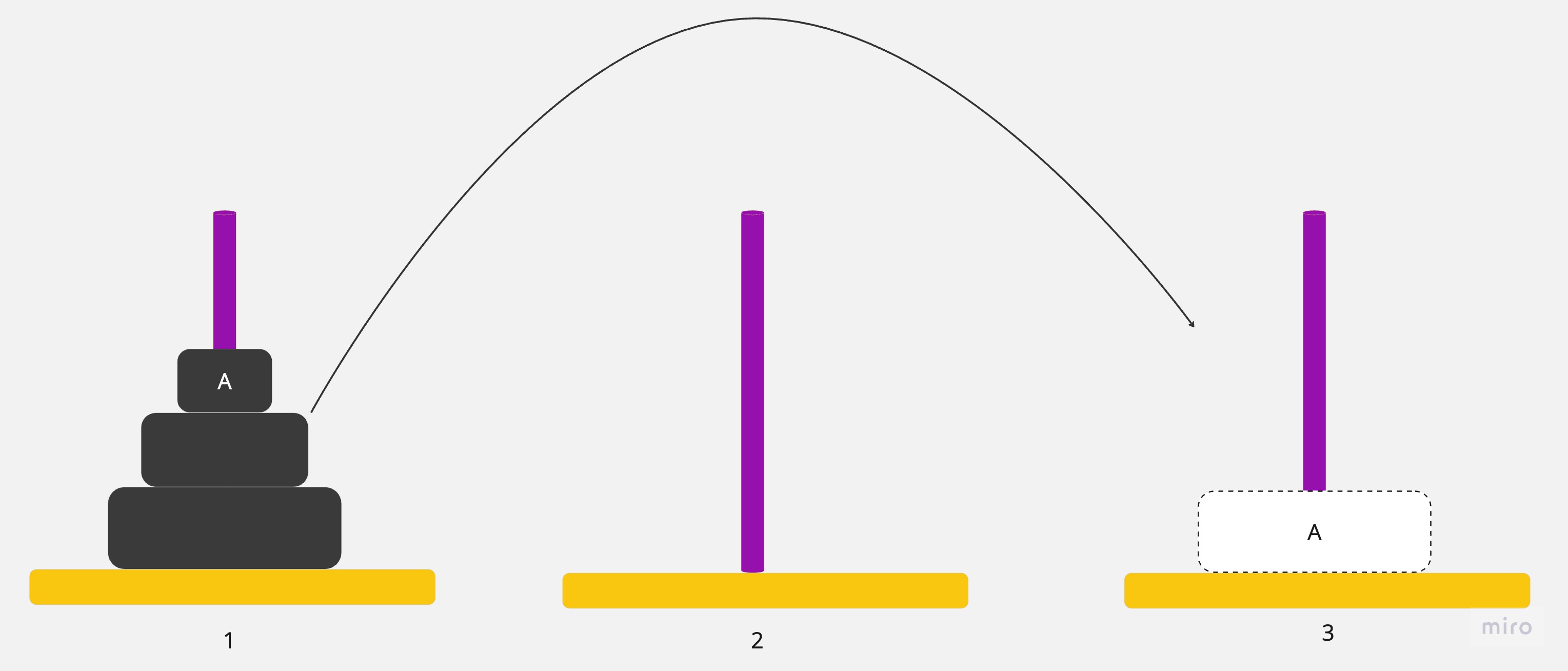
2.將圓盤從1號銀棒移到2號銀棒

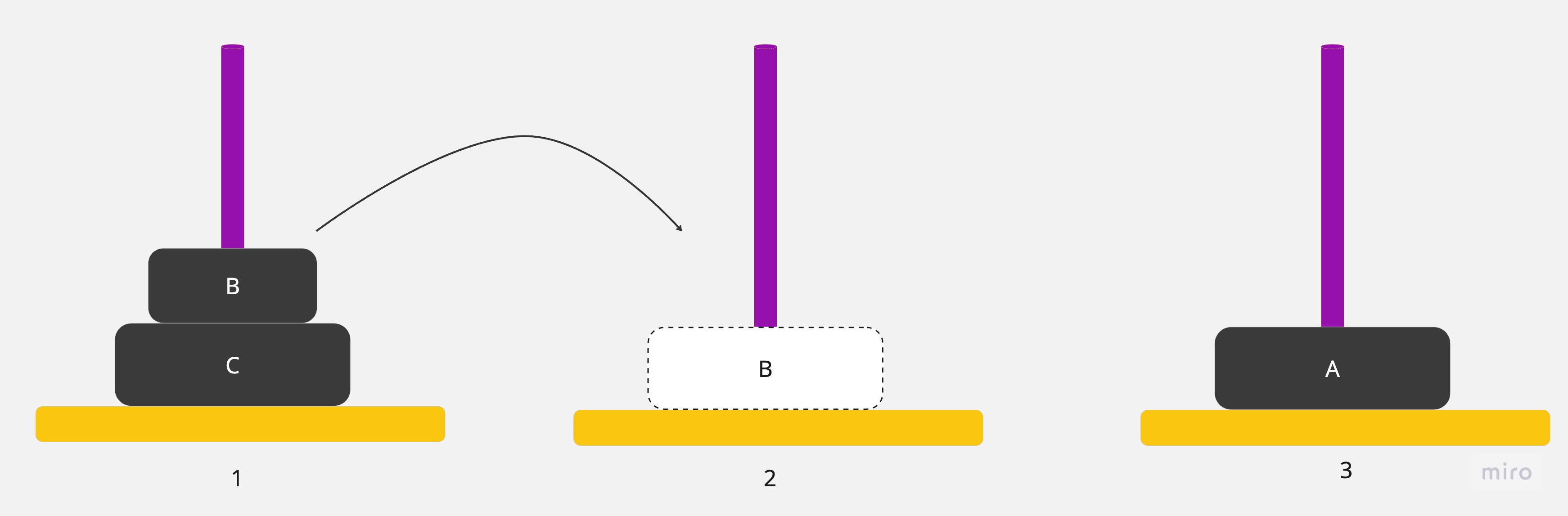
3.將圓盤從3號銀棒移到2號銀棒

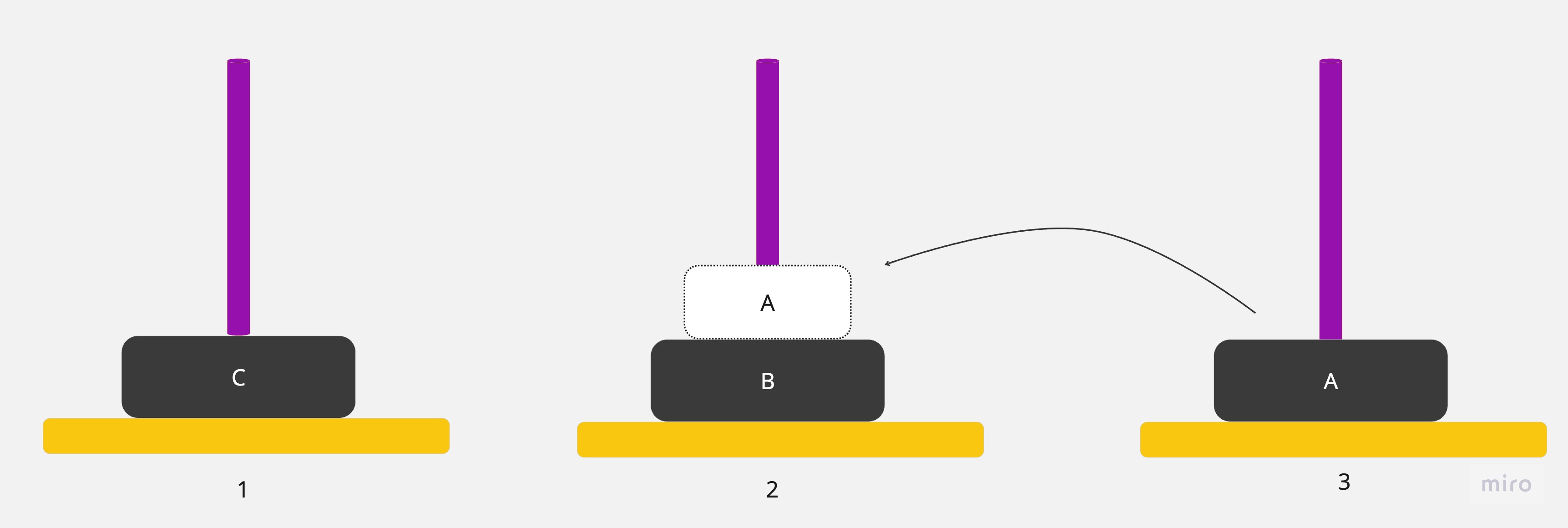
4.將圓盤從1號銀棒移到3號銀棒

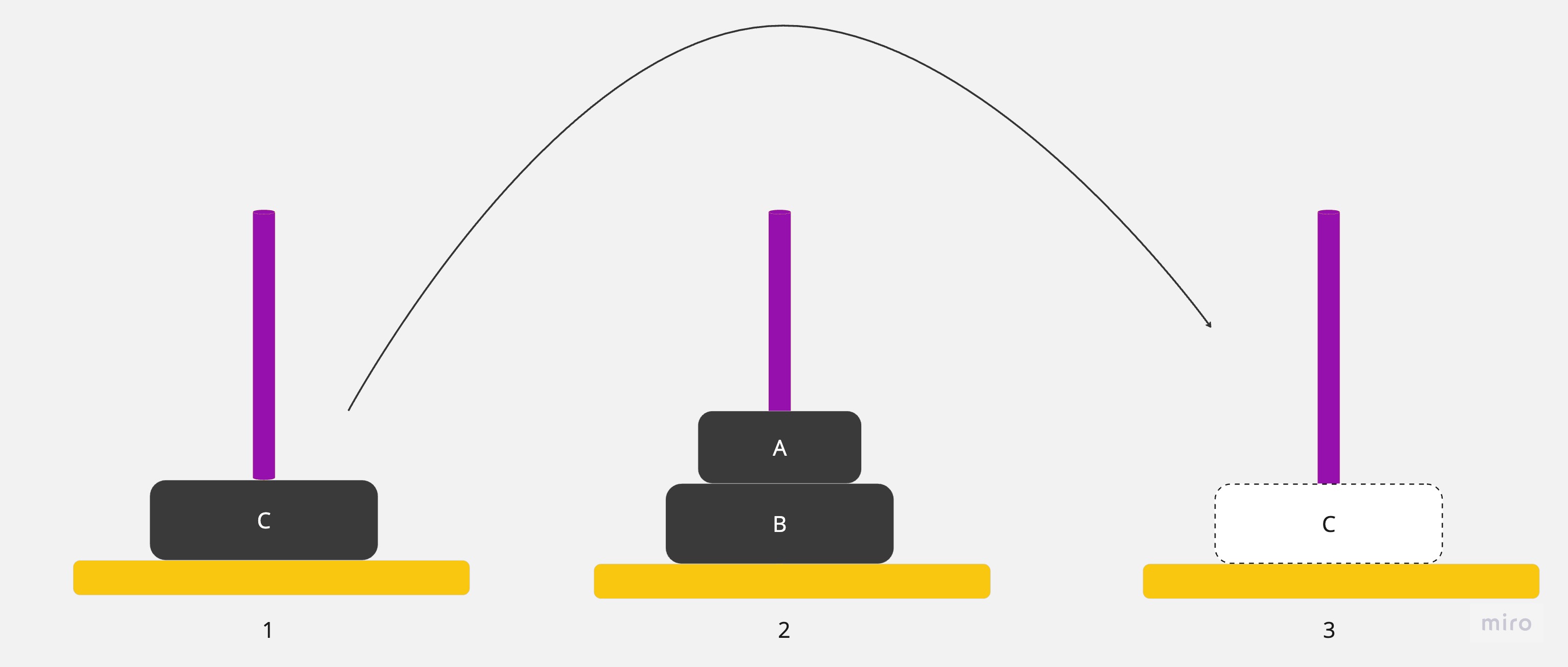
5.將圓盤從2號銀棒移到1號銀棒

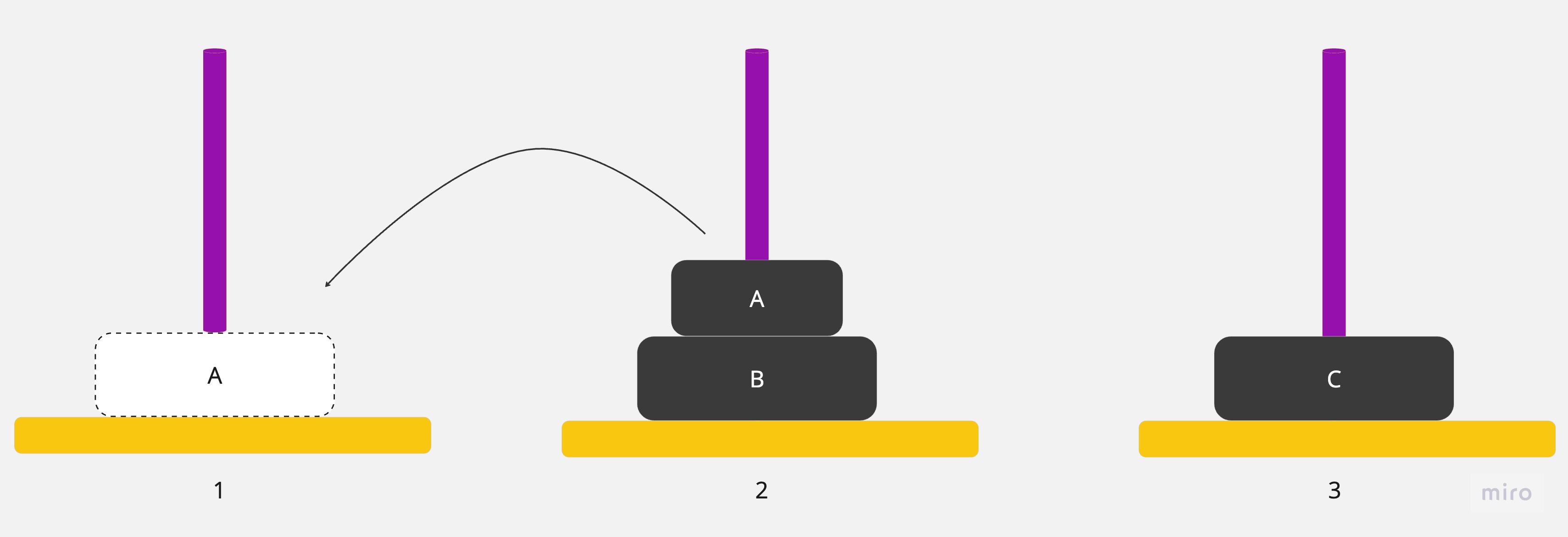
6.將圓盤從2號銀棒移到3號銀棒

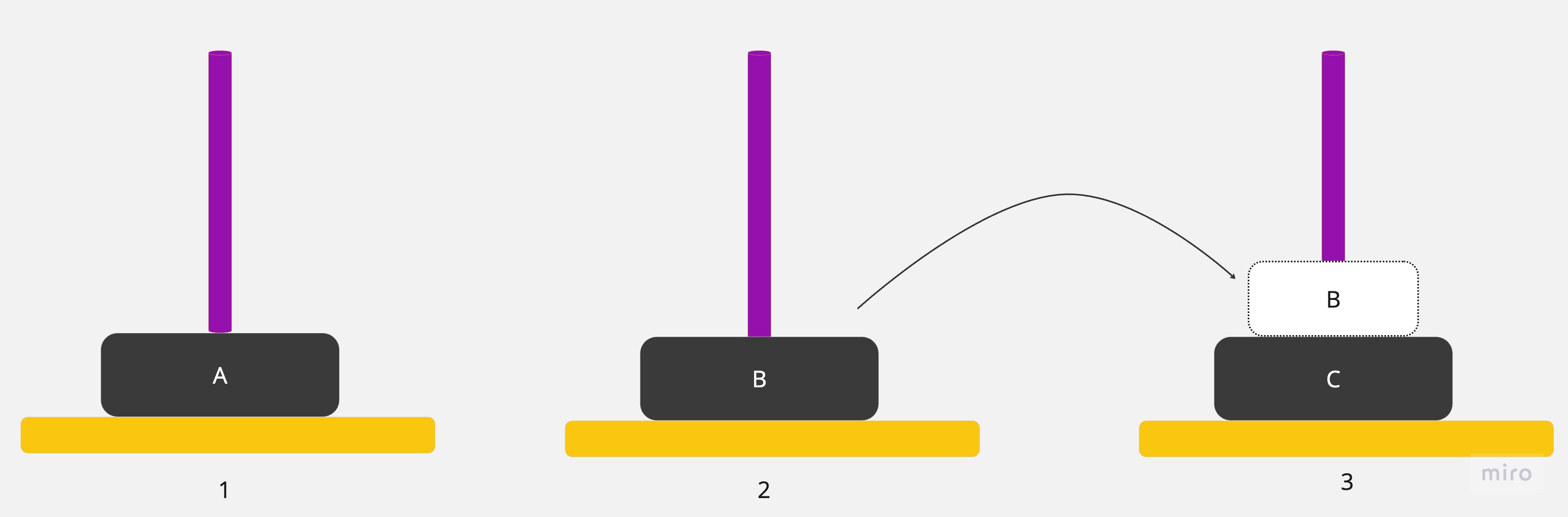
7.將圓盤從1號銀棒移到3號銀棒，就完成了。

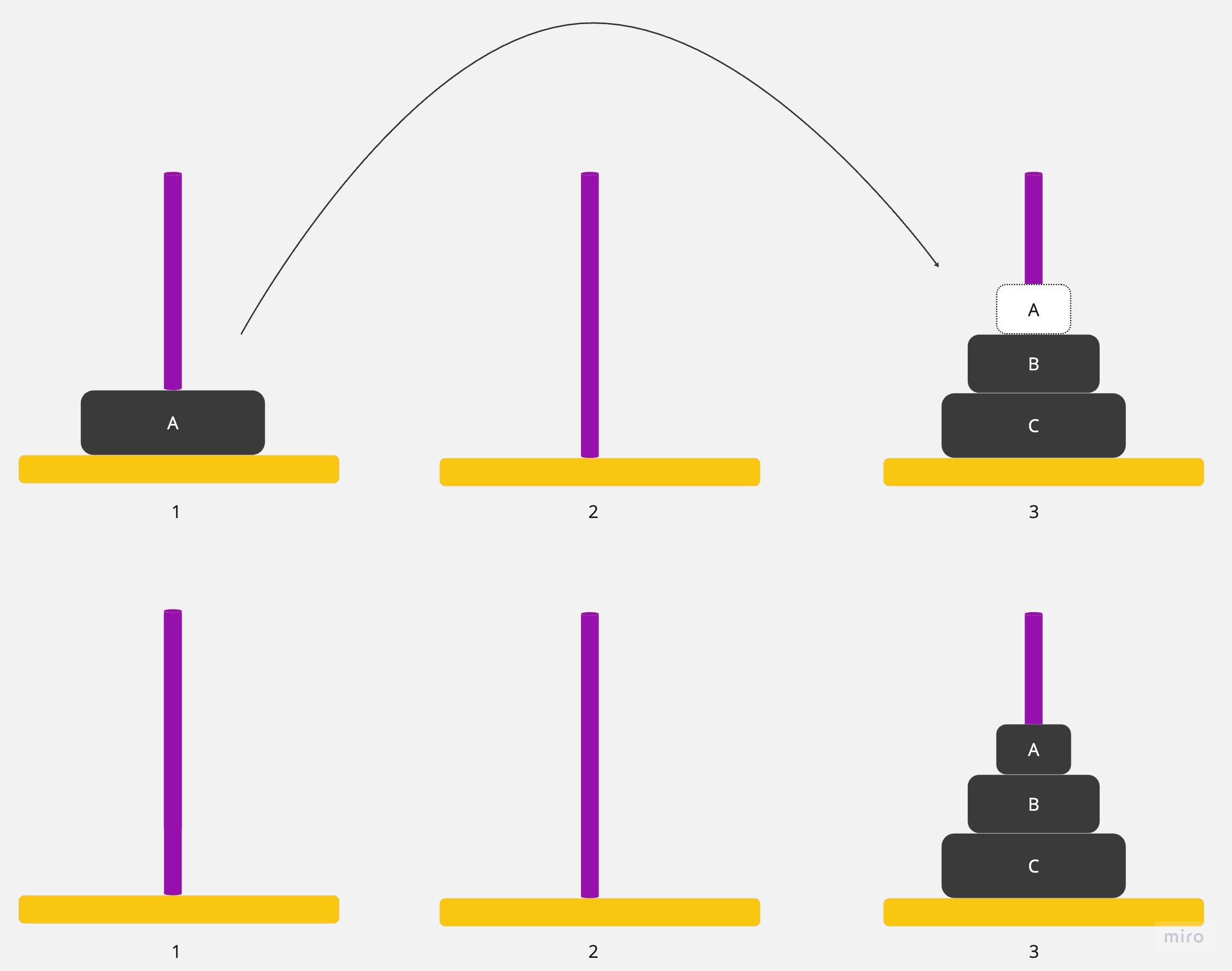
結論:移動了2^3-1=7次，圓盤移的順序為1,2,1,3,1,2,1(圓盤次序)

步驟:1>3,1>2,3>2,1>3,2>1,2>3,1>3(銀棒次序)

當n不大時，用圖示就很好解決，但n的值大時，就沒那麼方便用圖。

1.將n-1個圓盤，從銀棒1移動到2

2.將第n個最大圓盤從銀棒1移到3

3.將n-1個圓盤，從銀棒2移到3

河內塔這範例非常適合以遞迴與堆疊來解，主要是滿足了的特性:

1.有反覆執行的過程

2.有停止的出口

pub fn hanoi(n: usize, road_from: char, road_temp: char, road_to: char) {
    if n == 1 {
        println!("圓盤從 {} 移到 {} ", road_from, road_to);
    } else {
        hanoi(n - 1, road_from, road_to, road_temp);
    }
}

範例:

以遞迴方式來解河內塔:

fn hanoi(n: u32, road_from: char, road_temp: char, road_to: char) {
    if n == 1 {
        println!("圓盤 {} 從 {} 移到 {}", n, road_from, road_to);
        return;
    }

    hanoi(n - 1, road_from, road_to, road_temp);
    println!("圓盤 {} 從 {} 移到 {}", n, road_from, road_to);
    hanoi(n - 1, road_temp, road_from, road_to);
}

fn main() {
    let num_disks = 4; // 設置河內塔的圓盤数量
    hanoi(num_disks, 'A', 'B', 'C');
}