Floyd algorithm

相較於Dijkstra的方法只能求出某一點到其他頂點的最短距離，如果要求出圖形中任意兩點甚至所有頂點間最短的距離，就要用Floyd演算法。

Floyd演算法定義:

原理是動態規劃。設D_i,j,k為從i到j的只以(1..k)集合中的節點為中間節點的最短路徑的長度。

⑴ A^k[i][j]=min{A^k-1[i][j],A^k-1[i][k]+A^k-1[k][j]}，k>=1，k表示經過的頂點，A^k[i][j]為從頂點i到j經由k頂點的最短路徑。

⑵ A^0[i][j]=COST[i]j，A^0為頂點i到j間的直通距離。

⑶ A^[i,j]代表i到j的最短距離，即A^n是我們所要求的最短路徑成本矩陣。

拿下圖舉用，用Floyd來求得各頂點間的最短路徑。

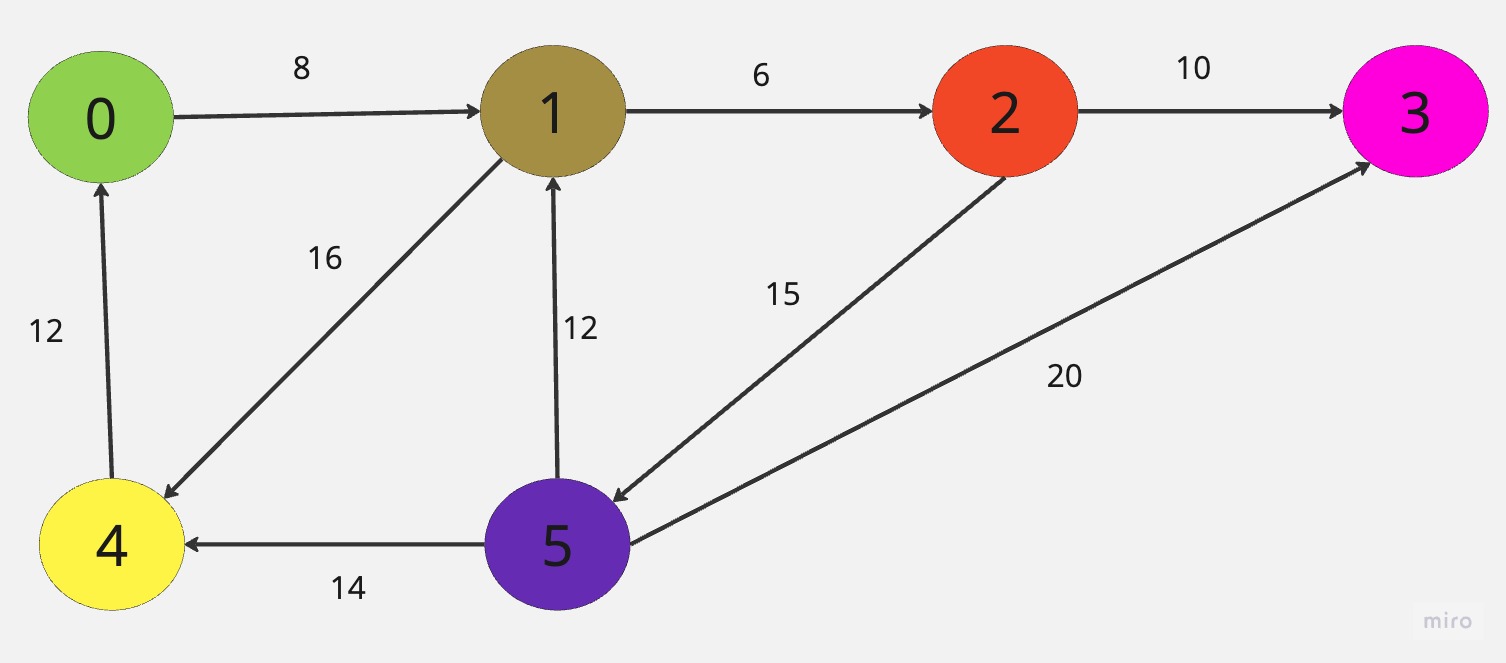
㈠找到A^0[i][j]=COST[i][j]，A^0為不經任何頂點的成本矩陣，若沒有路徑則以(無窮大)表示。

⑵ 找出A^0[i][j]由i到j，經由頂點㈠的最短距離，並填入矩陣，

A^0[1][2]=min{A^0[1][2],A^0[1][1]+A^0[1][2]}=min{4,0+4}=4

A^0[1][3]=min{A^0[1][3],A^0[1][1]+A^0[1][3]}=min{11,0+11}=11

A^0[2][1]=min{A^0[2][1],A^0[2][1]+A^0[1][1]}=min{6,6+0}=6

A^0[2][3]=min{A^0[2][3],A^0[2][1]+A^0[1][3]}=min{2,6+11}=2

A^0[3][1]=min{A^0[3][1],A^0[3][1]+A^0[1][1]}=min{3,3+0}=3

A^0[3][2]=min{A^0[3][2],A^0[3][1]+A^0[1][2]}=min{∞,3+4}=7

依序求到各頂點的值後可得到A^1矩陣:

⑶ 求出A^2[i][j]經由頂點⑵ 最短距離。

A^2[1][2]=min{A^1[1][2],A^1[1][2]+A^1[2][2]}=min{4,4+0}=4

A^2[1][3]=min{A^1[1][3],A^1[1][2]+A^1[2][3]}=min{11,4+2}=6

依序求其他各項頂點的值可得到A^2矩陣

⑷ 求出A^3[i][j]經由頂點⑶ 最短距離。

A^3[1][2]=min{A^2[1][2],A^2[1][3]+A^2[3][2]}=min{4,6+7}=4

A^3[1][3]=min{A^2[1][3],A^2[1][3]+A^2[2][3]}=min{6,6+0}=6

依序求其他各項頂點的值可得到A^3矩陣

完成所有矩陣間最短路徑為矩陣A^3所示。

由這個範例可知，一個加權圖形若有n個頂點，則此方法必須執行n次迴圈，逐一產生A^1,A^2,A^3….A^k個矩陣。

Floyd演算法:

fn floyd(&mut self) {
    let num_nodes = self.adjacency_matrix.len();

    // Floyd's Algorithm 主迴圈
    for k in 0..num_nodes {
    //每一個節點 k 做嘗試
        for i in 0..num_nodes {
        // 所有節點對 (i, j)
            for j in 0..num_nodes {
                if self.adjacency_matrix[i][k] != usize::MAX
                    && self.adjacency_matrix[k][j] != usize::MAX
                {
                    // 避免整數溢位
                    if let Some(new_dist) = self.adjacency_matrix[i][k].checked_add(
                        self.adjacency_matrix[k][j],
                    ) {
                        // 更新最短路徑
                        self.adjacency_matrix[i][j] =
                            self.adjacency_matrix[i][j].min(new_dist);
                    }
                }
            }
        }
    }
}