圖形演算法

前面也有介紹到圖形的定義，這邊會來介紹圖形的演算法。

圖形的走訪

前幾天的樹追蹤是拜訪樹的每一個節點一次，用的方法有前中後序法，那圖形追蹤的定義，就是G=(V,E)，我們從V開始，經由此節點相鄰的節點而去拜訪G中其他節點，稱為「圖形追蹤」。從某一個頂點V1開始，走訪可經由V1到達的頂點，接著再走訪下一個頂點直到全部的頂點走訪完畢。

在走訪過程可能會重複經過某些頂點及邊線。經由圖形的走訪可以判斷該圖形是否連通，並找出連通單元及路徑。

圖形走訪有兩種「先深後廣走訪」，「先廣後深走訪」。

先深後廣走訪（Depth-First Search）

先深後廣走訪類似前序走訪，從圖形的某一頂點開始走訪，被拜訪過的頂點就做上已拜訪的記號，接著走訪此頂點所有相鄰且未拜訪過頂點中的任意頂點，並做上已拜訪的記號，再以該點為新的起點繼續進行先深後廣的搜索。

這圖形追蹤結合了遞迴及堆疊兩種方法，由於會造成無窮迴圈，所以必須加入一個變數，判斷該點是否已經走訪完畢，這樣講還是很複雜吧，用圖看比較好懂走訪。

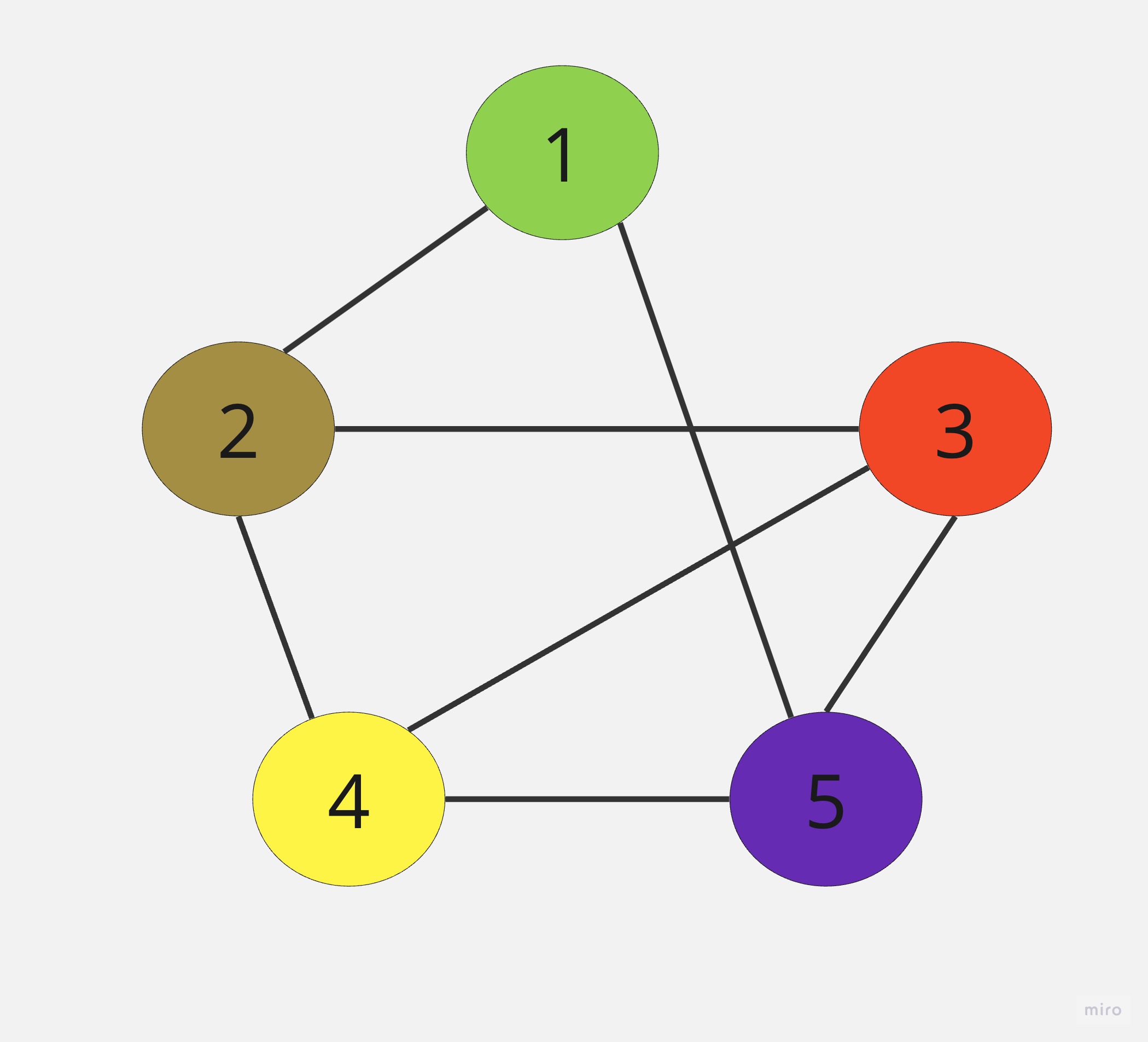
① 以頂點1為起點，將相鄰的頂點2及頂點5放入堆疊。

② 取出頂點2，將與頂點2相鄰且未拜訪過的頂點3及頂點4放入堆疊。

③ 取出頂點3，將與頂點3相鄰且未拜訪過的頂點4及頂點5放入堆疊。

④ 取出頂點4，將與頂點4相鄰且未拜訪過的頂點4及頂點5放入堆疊。

⑤ 取出頂點5，將與頂點5相鄰且未拜訪過的頂點放入堆疊，因為頂點5相鄰的頂點全部被拜訪過，所以無須再放入堆疊。

⑥ 將堆疊內的值取出並判斷是否已經拜訪過，直到堆疊內無節點可走為止。

先深後廣的走訪順序: 頂點1、頂點2、頂點3、頂點4、頂點5。

深度優先函數:

    let mut ptr = &head[current as usize];
    while let Some(link) = ptr {
        if run[link.val as usize] == 0 {
            dfs(link.val, run, head);
        }
        ptr = &link.next;
    }

先廣後深搜尋法（Breadth-First Search）

先廣後深是以佇列及遞迴來走訪，也是從某一圖形頂點開始走訪，被拜訪過的頂點就做上已拜訪的記號。所有相鄰且未拜訪過頂點中的任意一個頂點，並做上已拜訪的記號，再以該點為新的起點繼續進行先廣後深的搜尋。

① 以頂點1為起點，與頂點1相鄰且未拜訪過的頂點2及頂點5放入佇列。

② 取出頂點2，將與頂點2相鄰且未拜訪過的頂點3及頂點4放入佇列。

③ 取出頂點5，將與頂點5相鄰且未拜訪過的頂點3及頂點4放入佇列。

④ 取出頂點3，將與頂點3相鄰且未拜訪過的頂點4放入佇列。

⑤ 取出頂點4，將與頂點4相鄰且未拜訪過的頂點放入ㄓ佇列，因為頂點4相鄰的頂點全部被拜訪過，所以無須再放入佇列。

⑥ 將佇列內的值取出並判斷是否已經拜訪過，直到佇列內無節點可走為止。

先廣後深的走訪順序: 頂點1、頂點2、頂點5、頂點3、頂點4。

let mut queue = VecDeque::new();
    queue.push_back(start);

    while let Some(node) = queue.pop_front() {
        if run[node as usize] == 0 {
            run[node as usize] = 1;
            println!("[{}]", node);

            let mut ptr = &head[node as usize];
            while let Some(link) = ptr {
                if run[link.val as usize] == 0 {
                    queue.push_back(link.val);
                }
                ptr = &link.next;
            }
        }
    }