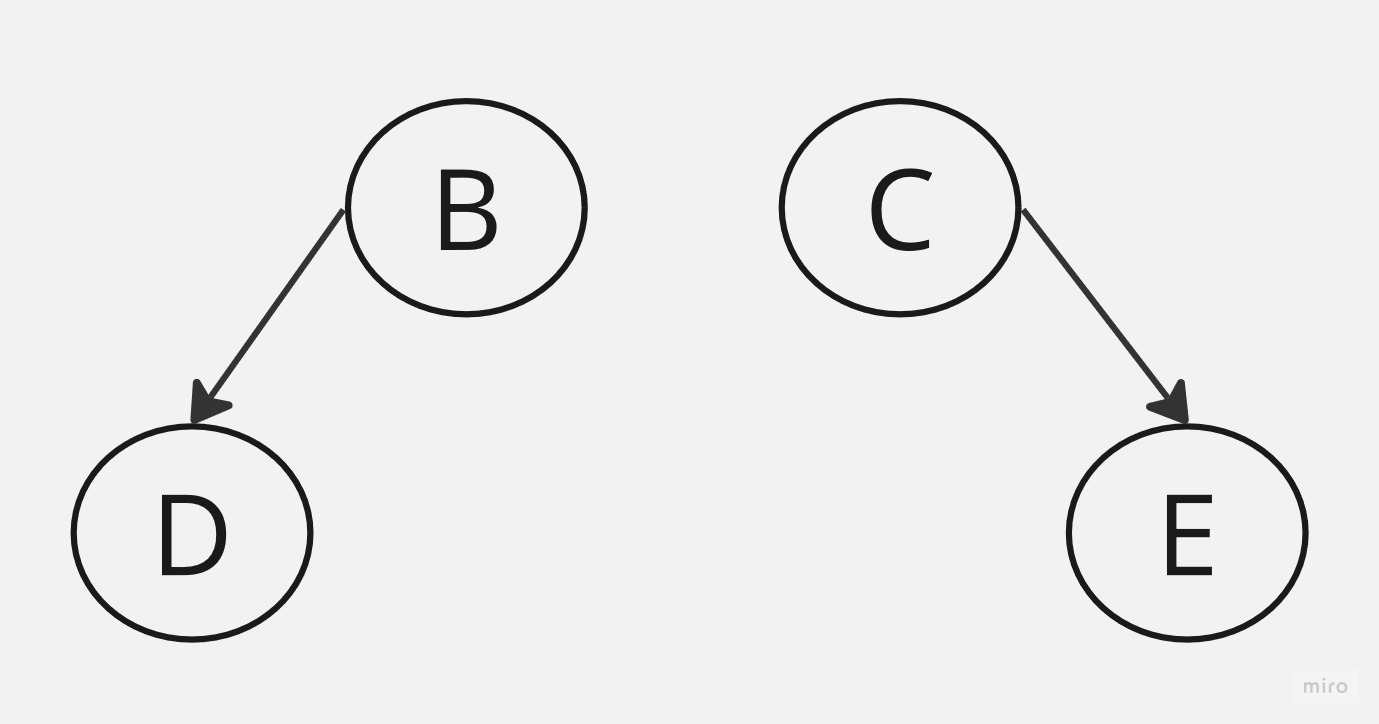
今天介紹資料結構中的樹狀結構，或稱樹狀圖(Tree Diagram)是一種將階層式的構造性質，以圖像方式呈現出來的方法。

樹的基本觀念

樹是由一個或多個節點(Node)組成，其中一個特定的節點稱為根節點(Root Node)，以及個不同節點相互連接，形成樹狀結構。

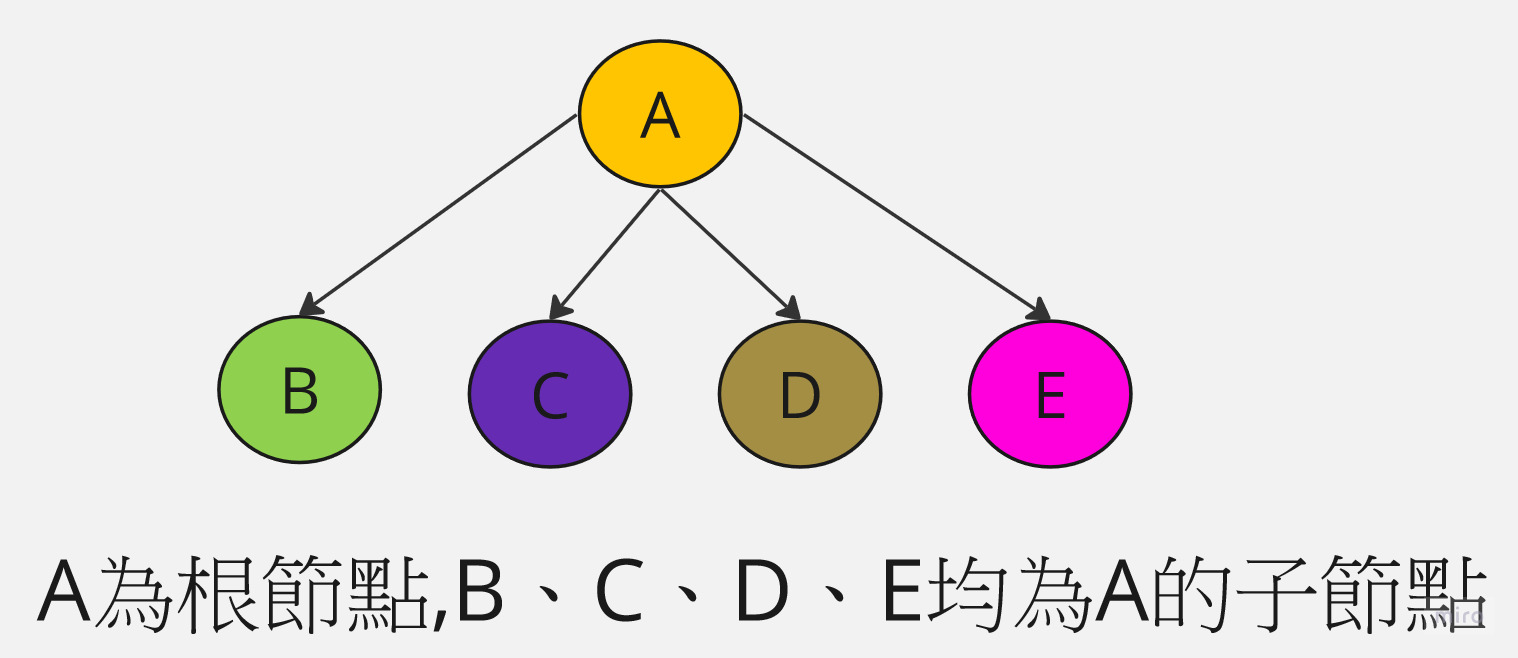
一顆合法的樹，節點可以互相連結，但不能形成無出口的迴圈。

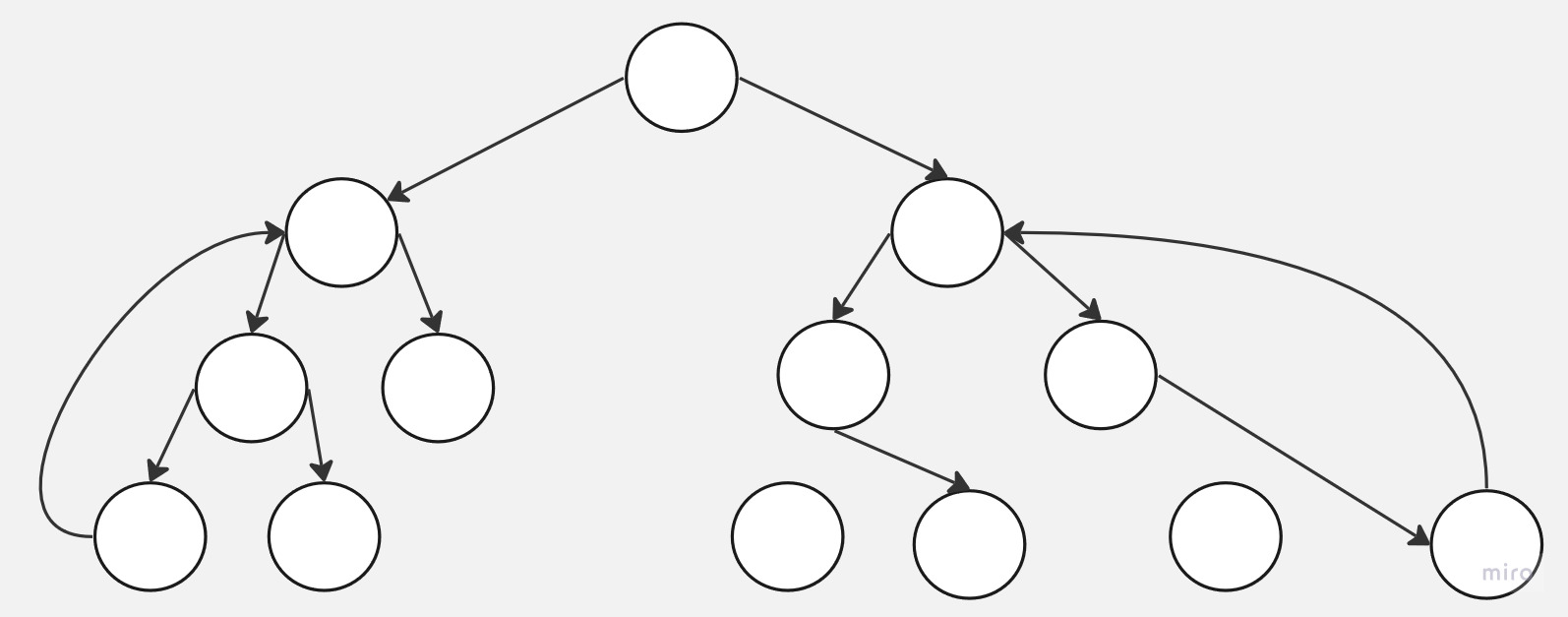
這就是一顆不合法的樹。

在樹狀結構的概念:

1.根節點(Root):沒有父節點的節點就是根節點

2.葉節點(Leaf):節點沒有子節點的節點即為葉節點

3.父節點(Parent):每個節點有連結的上一層節點為父節點

4.子節點(Children):每個節點有連結的下一層為子節點

5.祖先節點(Ancestor):指某節點到根節點之間所經過的所有節點

6.孫子節點(Descendant):該節點往上追朔子樹中的任一節點

7.兄弟節點(Siblings):有共同父節點的節點

8.非終端節點(Nonterminal Nodes):葉節點以外的其他節點

9.分支度(Degree):每個節點所有的子樹個數

10.階層(Level):樹的層級，如果樹根是1，其子節點是2，依序可以算出樹的階層數

11.高度(Height): 也稱為樹深(Depth)，指樹的最大階層數

12.同代(Generation):具有相同階層數的節點

13.樹林(Forest):由n個互斥樹的集合(n >= 0)，移去樹根即為樹林

二元樹

一般在電腦記憶體中的儲存方式是以鏈結串列為主，對於n元樹來說，因為每個節點的分支度都不相同，為了方便起見，我們必須取n為鏈結個數的最大固定長度。

這種N元樹會浪費鏈結空間，假設此n元樹有m個節點，那麼此樹共用了n * m個鏈結欄位。除了樹根外，每一個非空鏈結都指向一個節點，所以得知空鏈結個數為n * m-(m-1) = m * (n-1) +1，而n元樹的鏈結浪費率為m * (n-1) +1/ m * n。

當n=2時，2元樹的鏈結浪費率為1/2 當n=3時，3元樹的鏈結浪費率為2/3 當n=4時，4元樹的鏈結浪費率為3/4

當n = 2時，他的鏈結浪費率最低，所以為了改進浪費的缺點，我們就會使用二元樹結構來取代樹狀結構。

二元樹是由有限制點所組成的集合，可以為空集合或一個樹根及左右兩個子樹所組成。二元樹最多只能有兩個子節點，就是分支度小於或等於2。

二元樹跟樹是兩種不同的資料結構，可分為幾個差別:

1.節點分支數:

• 二元樹:每個節點最多有兩個子節點，一個左一個右節點

• 樹:每個節點有任意的子節點

2.結構特點:

• 二元樹:具有固定的分支結構，每個節點最多有兩個子節點

• 樹:每個節點可以有不同數量的子節點

這是一個以A為根節點的二元樹，包含了B,C為根節點的兩棵互斥的左子樹與右子樹。

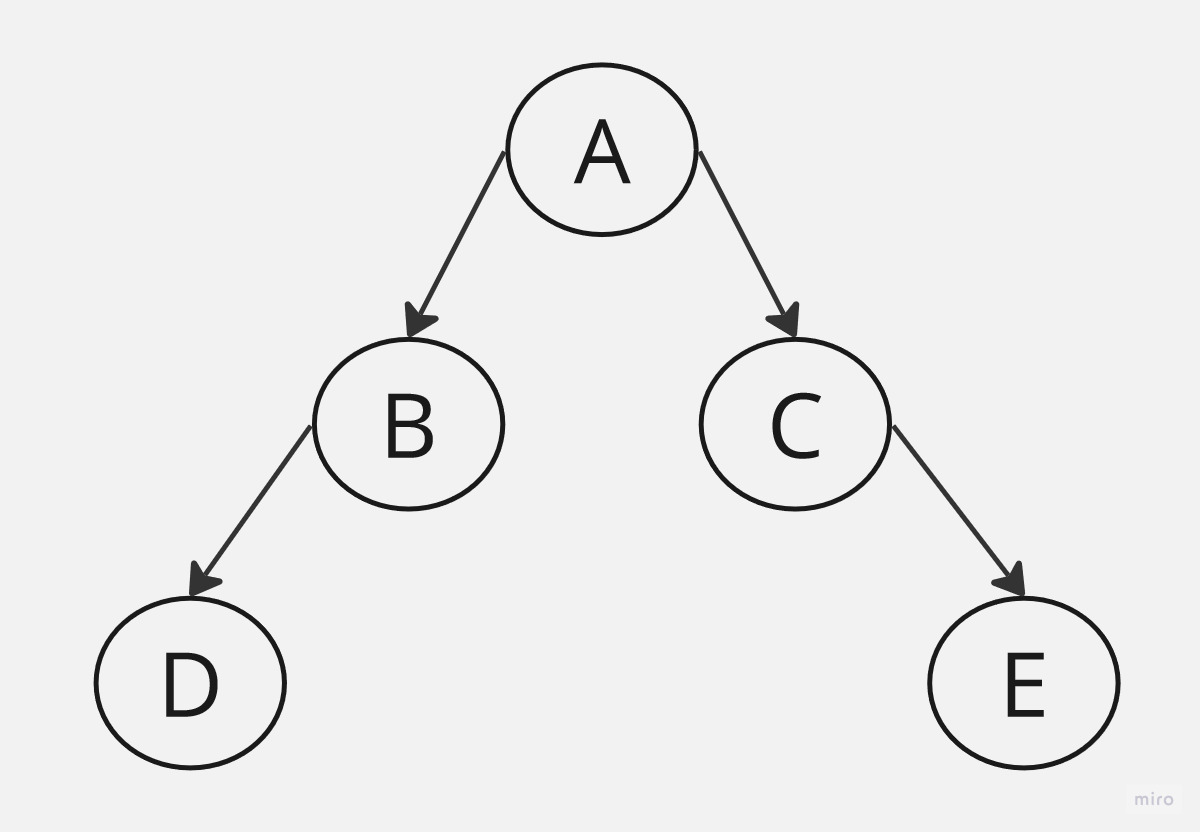
那這兩個左右子樹都是屬於同一個樹狀結構，不過卻是兩顆不同的二元樹結構，因為二元樹必須考慮到前後次序的問題。