樹狀演算法

前面有講過樹的基本概念和結構，這邊會講二元樹的應用，樹狀演算法大都是用鏈結串列來處理，鏈結串列的指標用來處理樹相當方便，只需改變指標即可，也可用陣列的連續記憶體來表示二元樹，至於使用陣列或鏈結串列有好有壞。

🌳 完滿二元樹(Full Binary Tree)

當二元樹的高度為h，樹的節點為2^-1，h>=0，則稱為「完滿二元樹」。

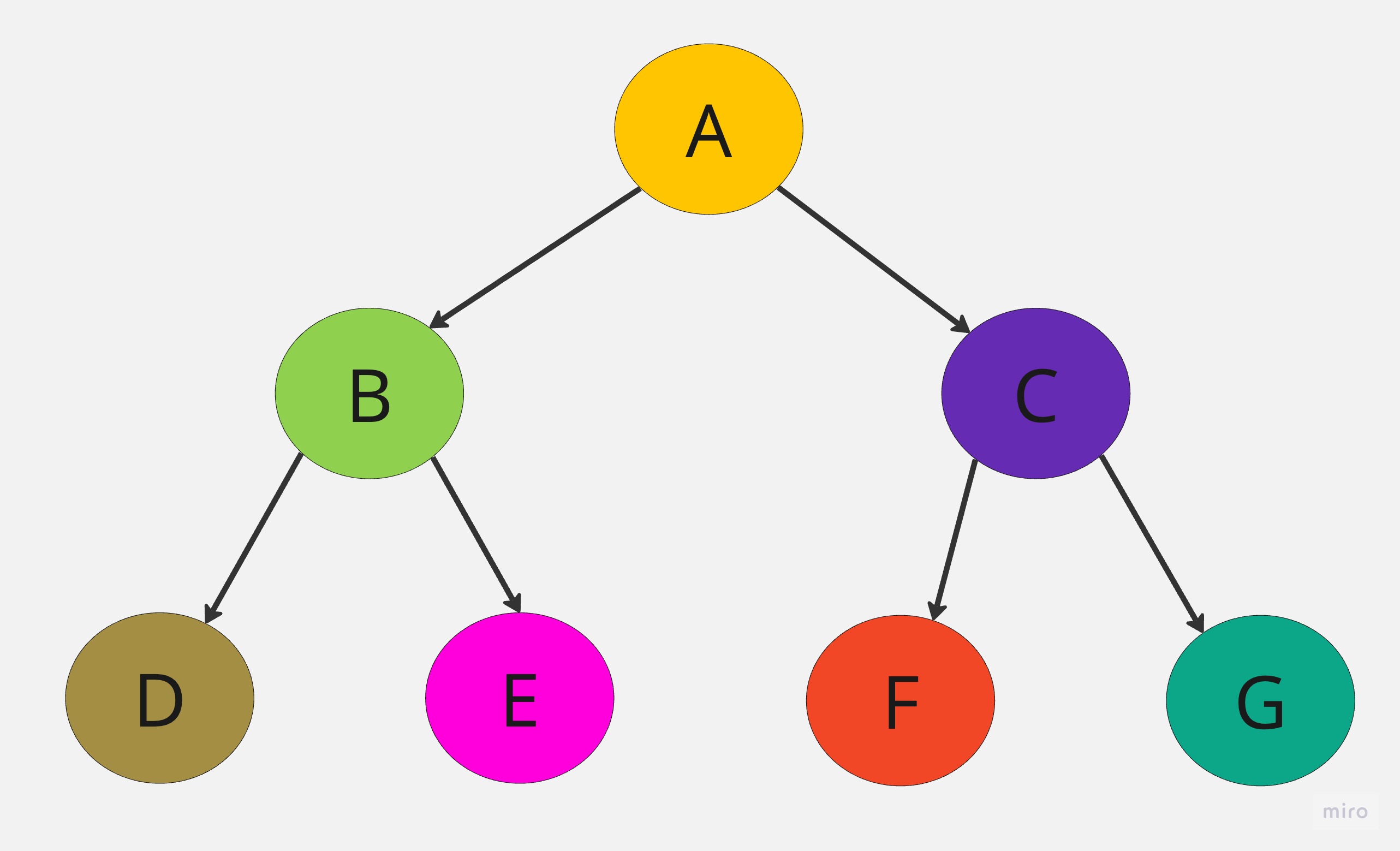
🌳 完整二元樹(Complete Binary Tree)

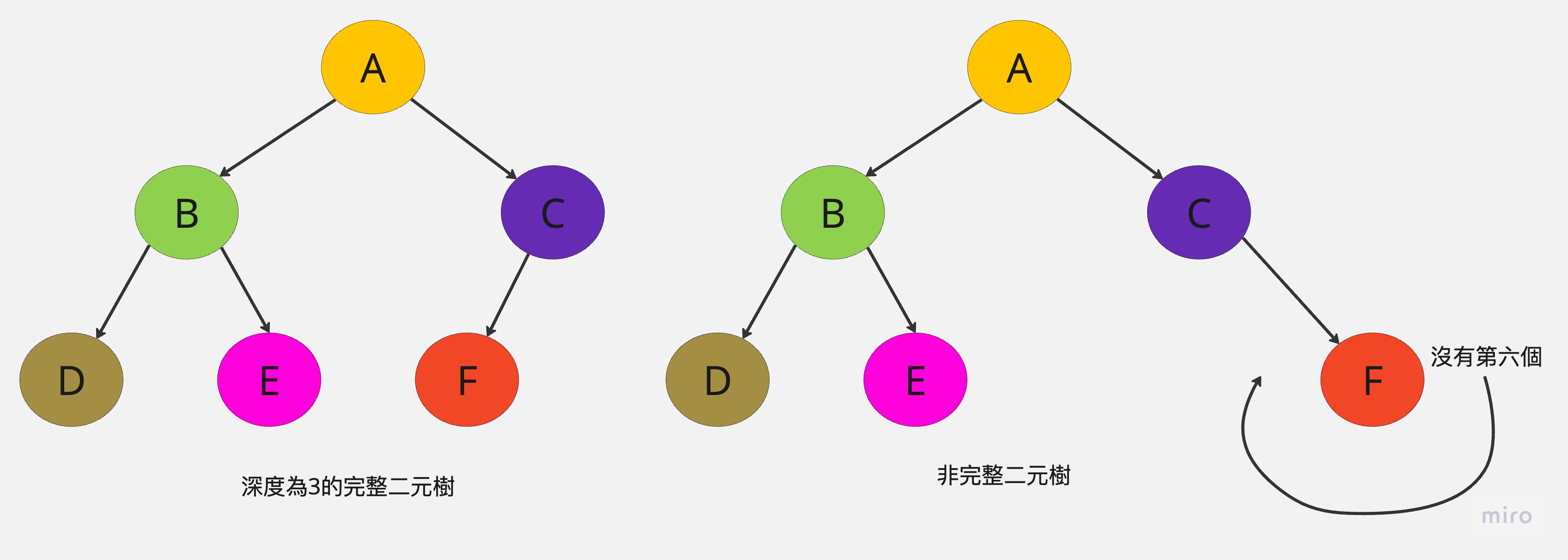
當二元樹的深度為h，所含的節點數小於2^h-1，其節點的編號方式如同深度h的完滿二元樹一樣，從左到右，由上到下的順序一一對應。

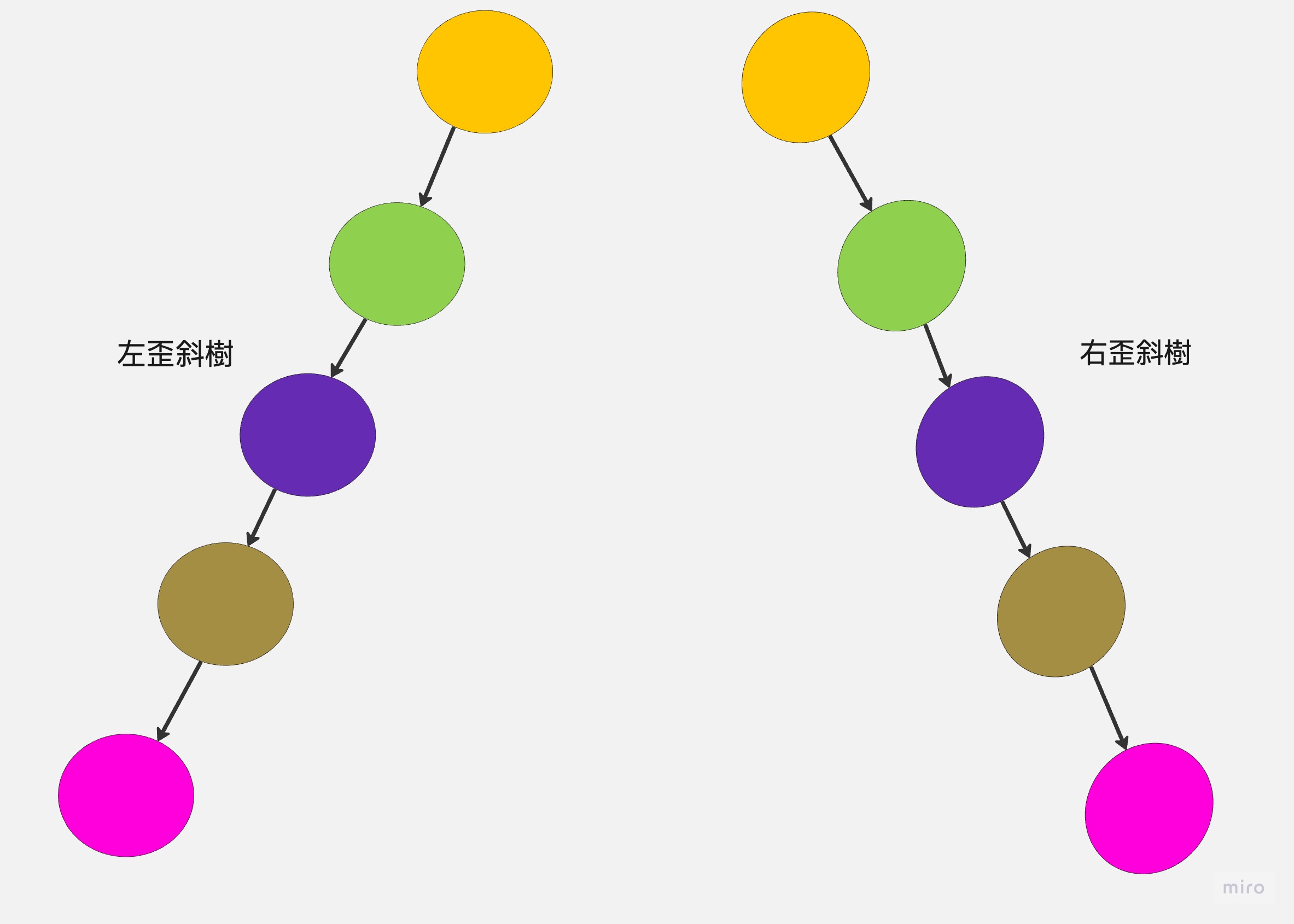
🌳 歪斜樹(Skewed Binary Tree)

當一個二元樹完全沒有左節點或右節點時，則稱為左歪斜樹或右歪斜樹。

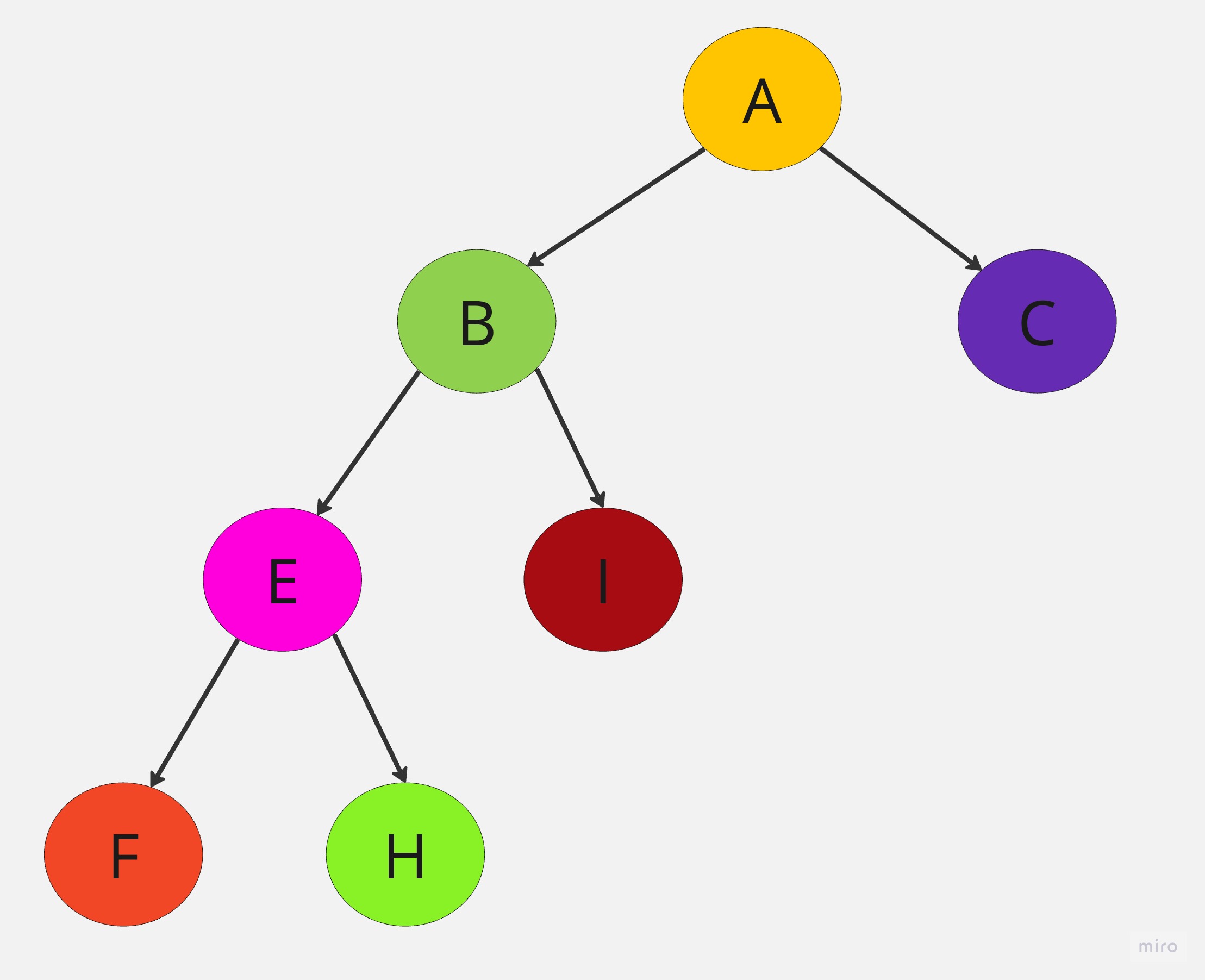
🌳 嚴格二元樹(Strictly Binary Tree)

指二元樹的每個非終端點均有非空的左右子樹。

陣列實作二元樹

使用循序的一維陣列表示二元樹，先將此二元樹想成一個完滿二元樹，且第n個階度具有2^n-1個節點，並依序存放在此一維陣列中。

先來看看使用一維陣列建立二元樹的表示方法及索引值的配置:

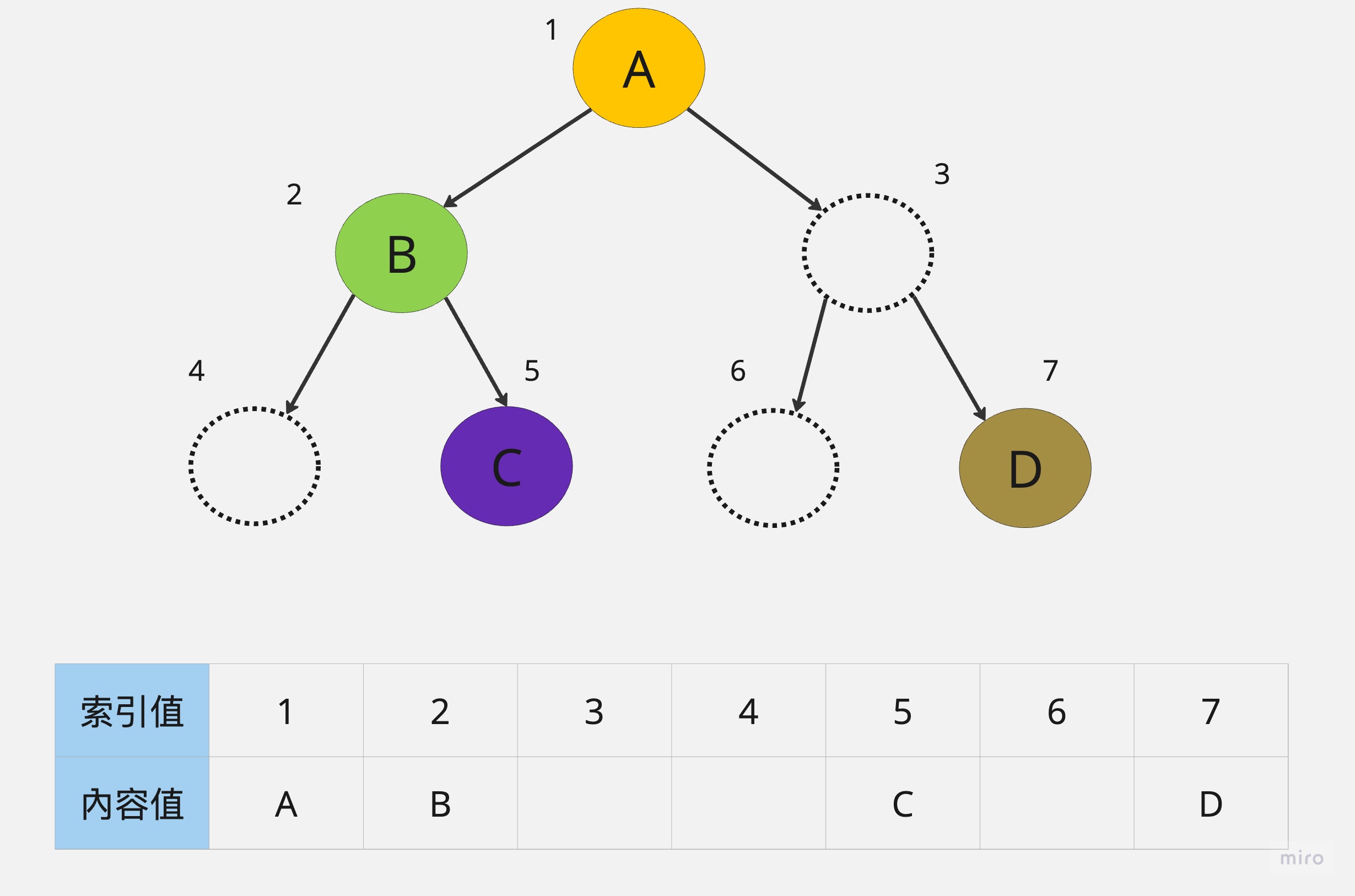
可以看到此一維陣列的索引值的關係

1. 左子樹索引值是父節點索引值 * 2。

2. 右子樹索引值是父節點索引值 * 2+1。

這邊來看如何以一維陣列建立二元樹，也就是建立一個二元搜尋樹，是很好的排序應用模式，因為在建立二元樹時，資料已經有初步的比較判斷，並依照二元樹的建立規則來存放資料。

二元搜尋樹特點:

🪴 可以是空集合，但若不是空集合則節點上一定要有一個鍵值。

🪴 每一個樹根的值需大於左子樹的值。

🪴 每一個樹根的值需小於右子樹的值。

🪴 左子樹也是二元搜尋樹。

🪴 樹的每個節點值都不相同。

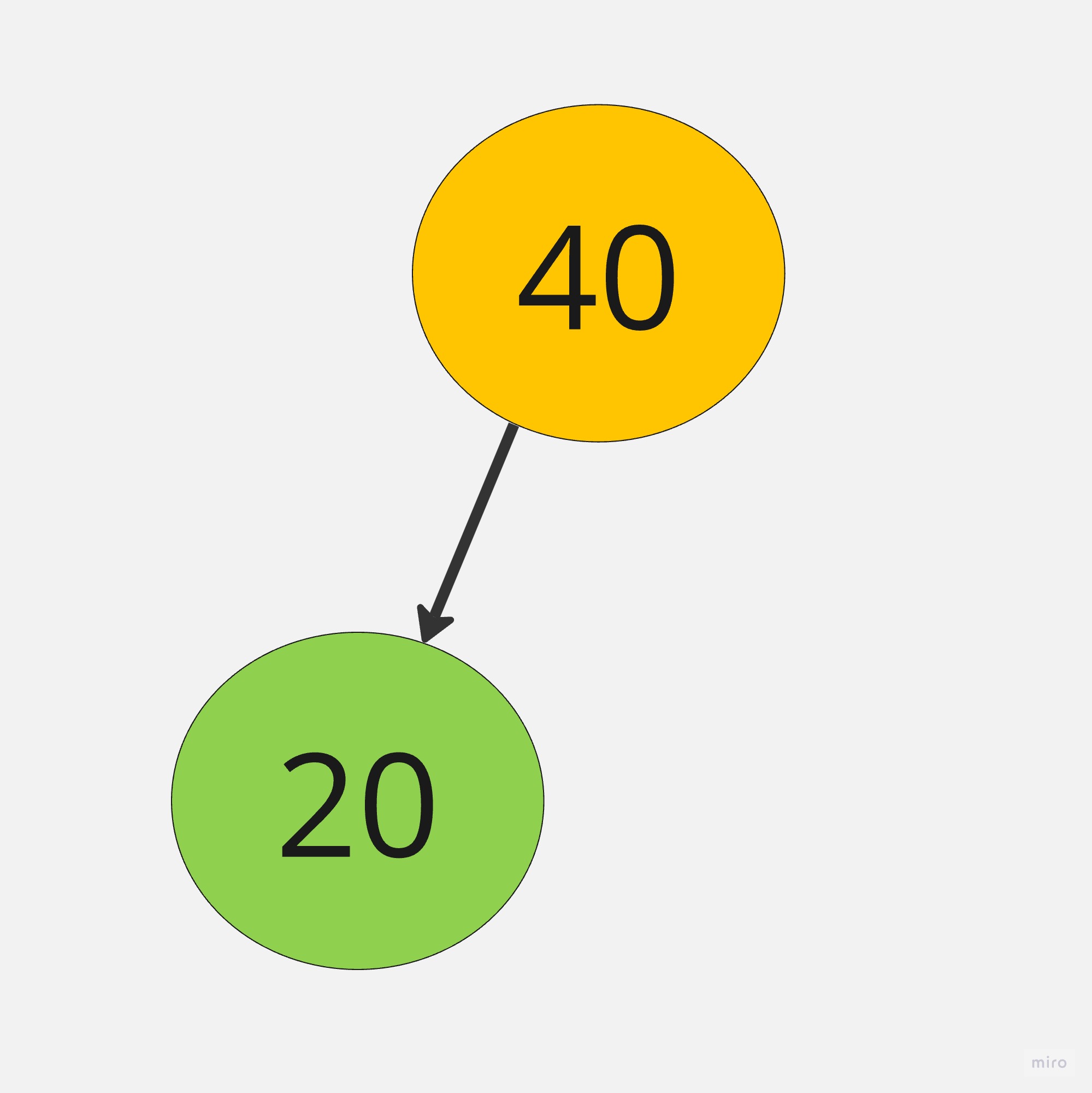
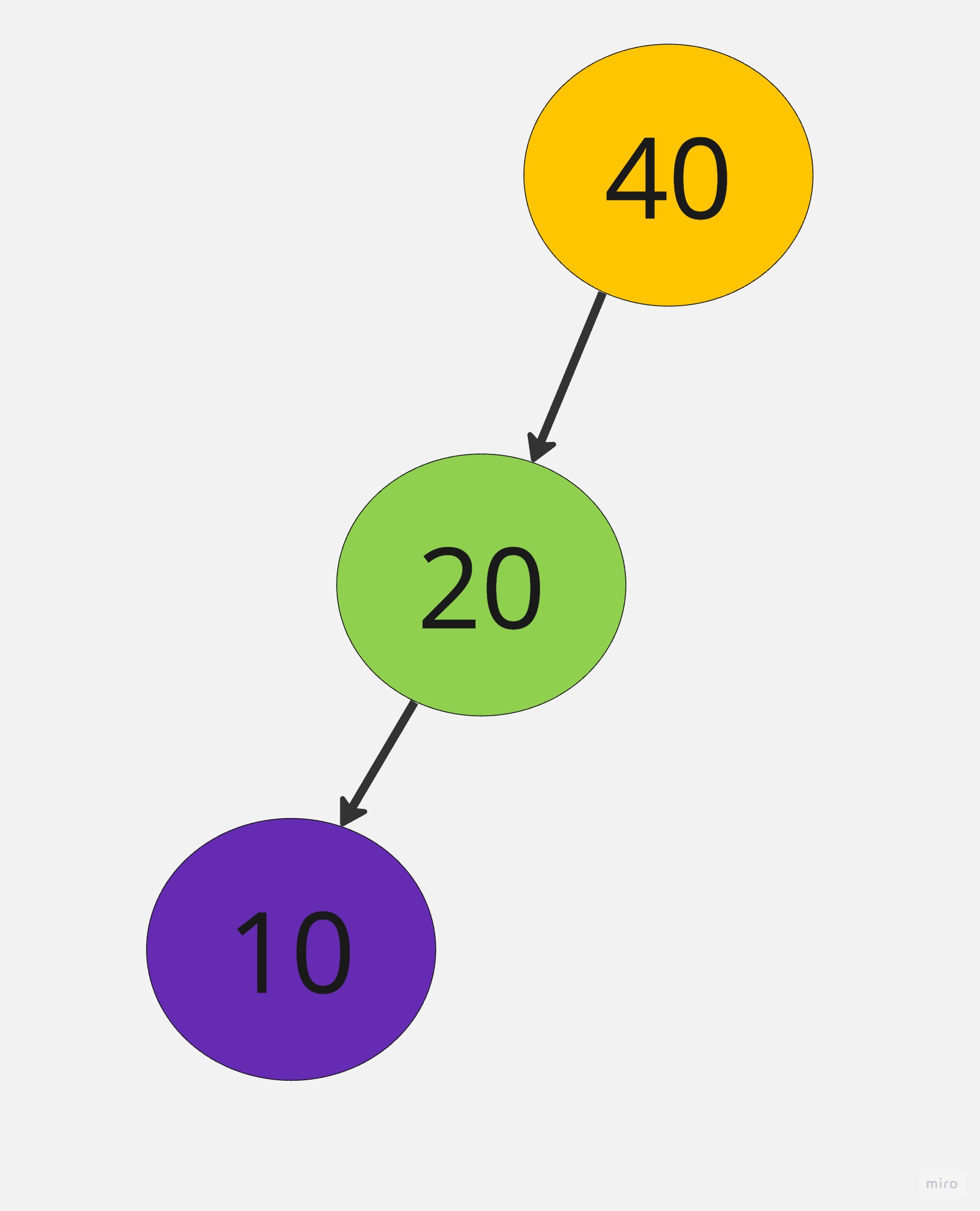
將一組資料40,20,10,50,30，建立一顆二元搜尋樹

1.

2.

3.

4.

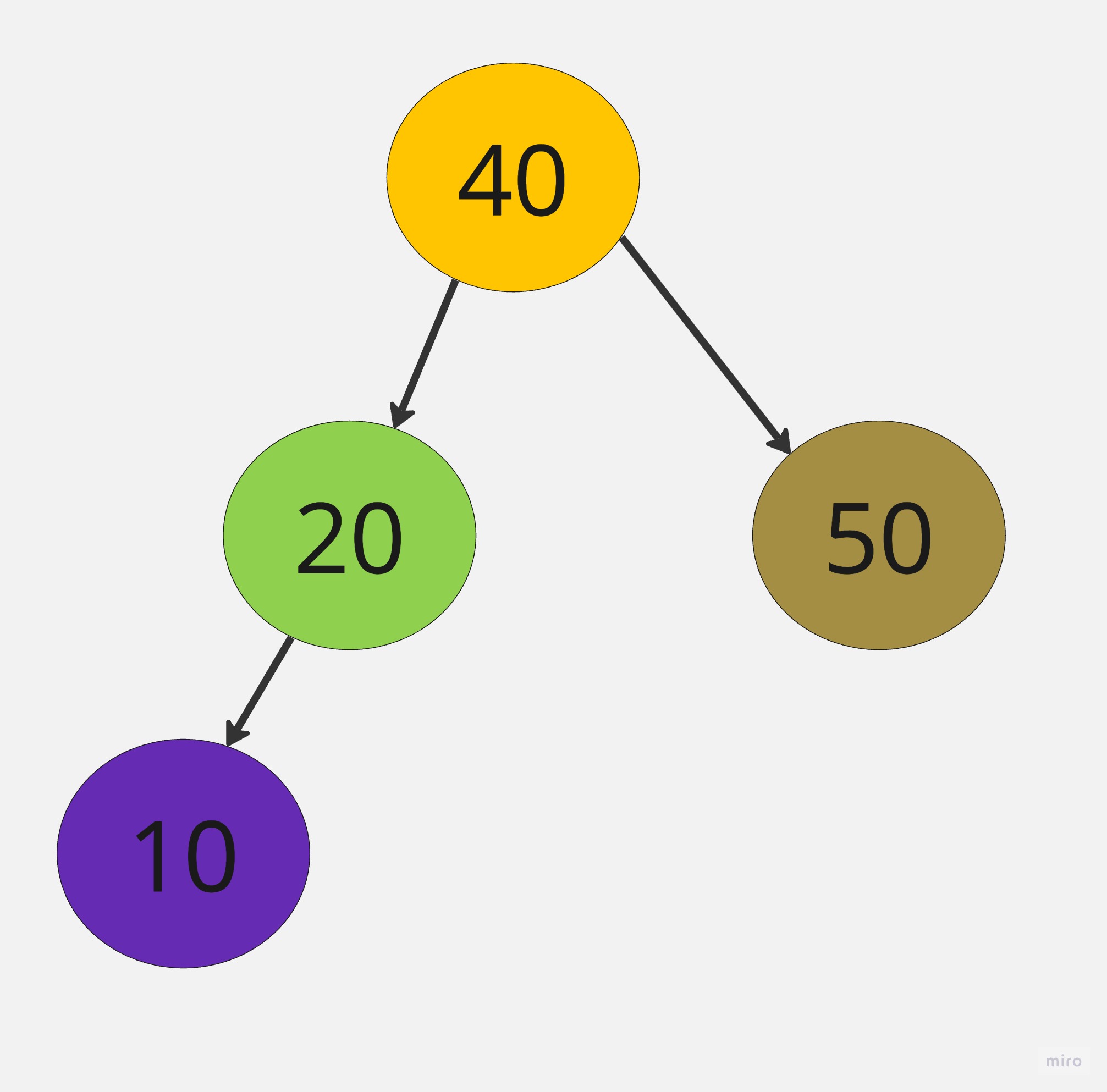
5.

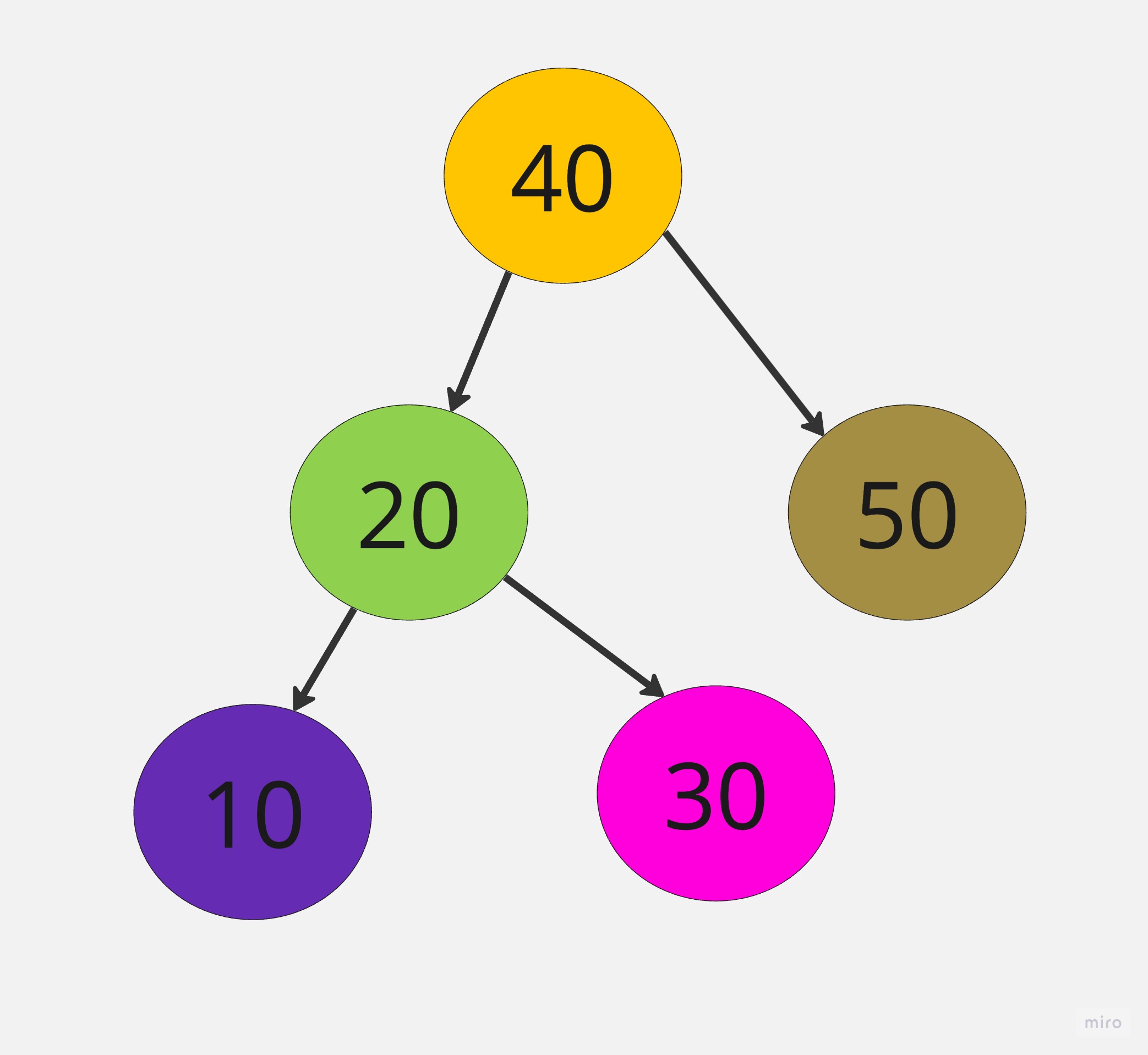
範例:

輸入一顆二元樹節點的資料為[40,20,10,50,30]

// 定義一個二元樹節點
struct TreeNode {
    data: i32,
    left: Option<Box<TreeNode>>,
    right: Option<Box<TreeNode>>,
}

impl TreeNode {
    fn new(data: i32) -> Self {
        TreeNode {
            data,
            left: None,
            right: None,
        }
    }

    // 插入數據到二元搜尋樹
    fn insert(&mut self, data: i32) {
        if data < self.data {
            if let Some(left) = &mut self.left {
                left.insert(data);
            } else {
                self.left = Some(Box::new(TreeNode::new(data)));
            }
        } else {
            if let Some(right) = &mut self.right {
                right.insert(data);
            } else {
                self.right = Some(Box::new(TreeNode::new(data)));
            }
        }
    }
    
    
    fn to_array(&self, array: &mut Vec<i32>) {
        if let Some(left) = &self.left {
            left.to_array(array);
        }
        array.push(self.data);
        if let Some(right) = &self.right {
            right.to_array(array);
        }
    }
}

fn main() {
    let data = vec![40,20,10,50,30];

    // 創建一個空的二元搜尋樹
    let mut root: Option<Box<TreeNode>> = None;

    // 依次插入數據
    for value in data.iter() {
        if let Some(ref mut node) = root {
            node.insert(*value);
        } else {
            root = Some(Box::new(TreeNode::new(*value)));
        }
    }

    // 轉化二元搜尋樹為一維陣列
    let mut result = Vec::new();
    if let Some(ref node) = root {
        node.to_array(&mut result);
    }

    println!("{:?}", result);
}