滿滿的演算法嗎？？

演算法是計算機科學與程式設計領域中重要的。也是我們人利用電腦解決問題的技巧之一，但不僅用於電腦領域上，包括數學、物理或是生活和工作都可以用演算法來描述．

接下來可能會說說演算法的意思，但知道有時候幾個字或是程式碼會讓人不太懂，所以會用圖解的方式來讓人來理解，但會介紹比較普遍的演算法或是常使用的為主．

演算法定義

演算法被定義為: 「 在有限步驟內解決數學問題的程式．」運用在計算領域中，我們也可以把演算法定義成: 「為了解決某個工作或問題，所需要有限數目的機械性或重複性指令與計算步驟． 」

演算法的條件

描述演算法所需五個條件．

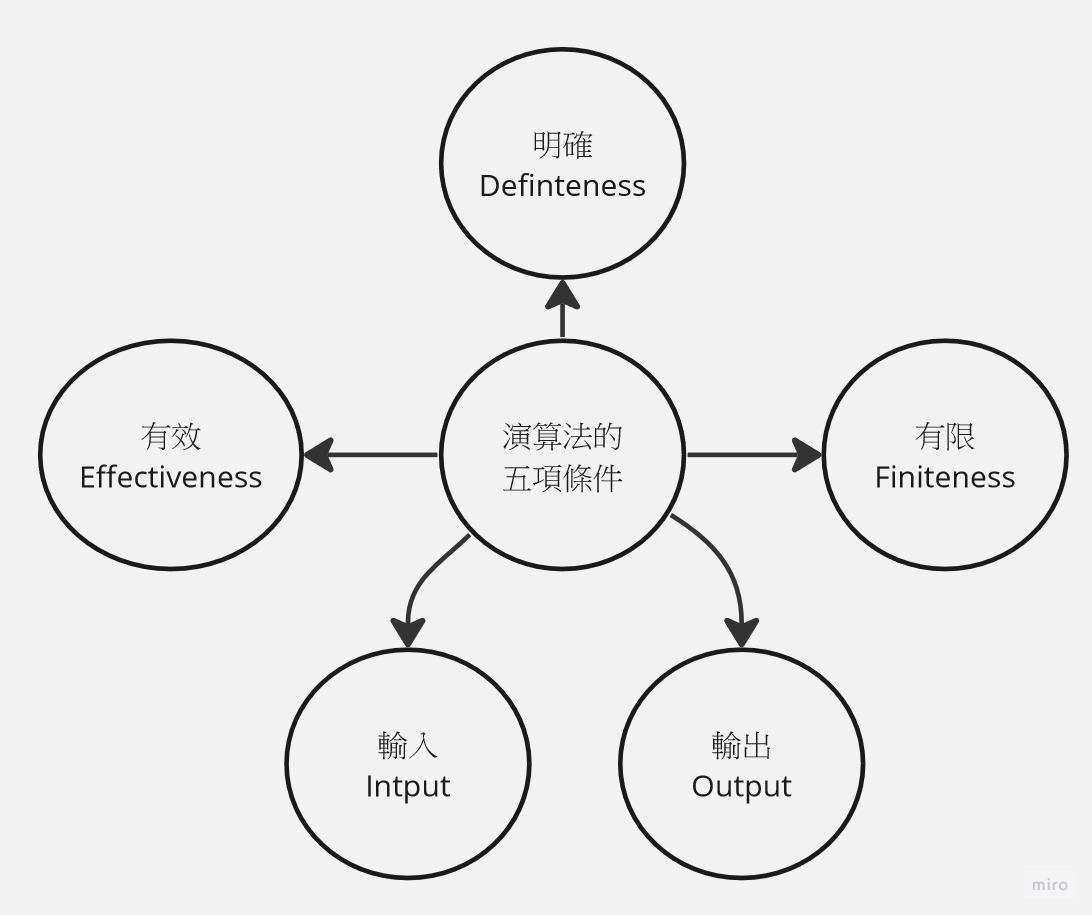
演算法特性	內容&說明
輸入(Input)	0個或多個輸入資料，這些輸入必須有清楚的描述或定義
輸出(Output)	至少會有一個輸出結果，不可以沒有輸出結果
明確性(Definiteness)	每一個指令或步驟必須是簡潔明確而不含糊的
有限性(Finiteness)	在有限步驟後一定會結束，不會產生無窮迴路
有效性(Effectiveness)	步驟清楚且可行，能讓使用者用紙筆計算而求出答案

另外流程圖(Flow Diagram)也是相當通用的演算法表示法，使用某些圖形符號．

時間複雜度O(f(n))

要如何評量一個演算法的好壞呢？

可以就某個演算法的執行步驟來衡量執行時間的標準，涉及到變數儲存與運算式的複雜度，真正絕對精確的執行時間一定不一樣． 可以利用一種「概量」的觀念來衡量執行時間，稱為「時間複雜度」(Time Complexity)

O(f(n))可視為某演算法在電腦中所需執行時間不會超過某一常數倍的f(n)，也就是當某演算法執行時間T(n)的時間複雜度．

時間複雜度只是執行次數的一個概略的量度層級，並非真的執行次數。而Big-oh是一種來表示最壞執行時間的表現方式，也是最常使用在描述時間複雜度的漸進式表示法． 常見的Big-oh有下列:

Big-oh	特色&說明
O(1)	稱為常數時間(constant time)，表示演算法的執行時間是一個常數倍
O(n)	稱為線性時間(linear time)，執行時間會隨著資料集合的大小而線性成長
O(log_2n)	稱為次線性時間(sub-linear time)，成長速度比線性時間還慢，而比常數時間還快
O(n^2)	稱為平方時間(quadratic time)，演算法的執行時間會成二次方的成長
O(n^3)	稱為立方時間(cubic time)，演算法的執行時間會成三次方成長
(2^n)	稱為指數時間(exponential time)，演算法的執行時間會成2的n次方成長
O(nlog_2n)	稱為線性成對數時間，介於線性及二次方程長的中間之行為模式

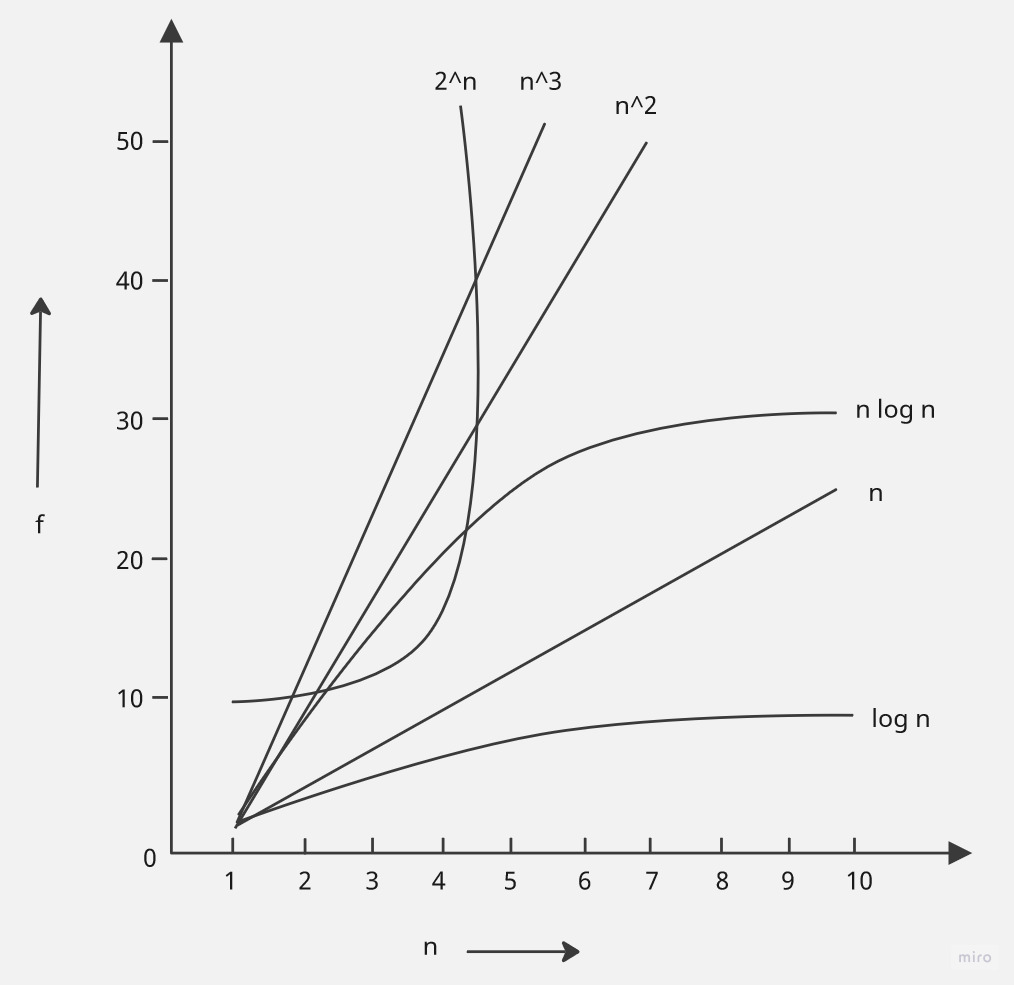
對於n>=16時ｍ時間複雜度的優劣比較關係如:

    O(1) < O(log_2 n) < O(n) <O(nlog_2 n) < O(n^2) < O(n^3) < O(2^n)